题目内容
如图,已知A,B分别为椭圆
+
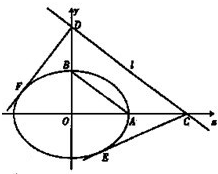
=1(a>b>)的右顶点和上顶点,直线 l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE•kDF等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A.±
| B.±
| C.±
| D.±
|

依题意,不妨令CD与该椭圆相切,切点为H,则切点F与H关于y轴对称,切点E与H关于x轴对称,如图,
∵kAB=-
,直线 l∥AB,
∴kCD=-
,
∴kDF=
(切点F在第二象限),或kDF=-
(切点F在第一象限);
同理可得,kCE=
(切点E在第四象限),或kCE=-
(切点E在第一象限);
∴CE与DF的斜率之积kCE•kDF=±
.
故选:C.

∵kAB=-
| b |
| a |
∴kCD=-
| b |
| a |
∴kDF=
| b |
| a |
| b |
| a |
同理可得,kCE=
| b |
| a |
| b |
| a |
∴CE与DF的斜率之积kCE•kDF=±
| b2 |
| a2 |
故选:C.


练习册系列答案
相关题目
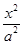 -
-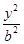 =1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )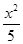 -
-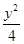 =1
=1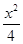 -
-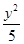 =1
=1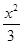 -
-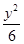 =1
=1 -
-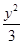 =1
=1