题目内容
设向量
,
的夹角为60°且|
|=|
|=1,如果
B=
+
,
C=2
+8
,
D=3(
-
).
(1)证明:A、B、D三点共线.
(2)试确定实数k的值,使k的取值满足向量2
+
与向量
+k
垂直.
| e1 |
| e2 |
| e1 |
| e2 |
| A |
| e1 |
| e2 |
| B |
| e1 |
| e2 |
| C |
| e1 |
| e2 |
(1)证明:A、B、D三点共线.
(2)试确定实数k的值,使k的取值满足向量2
| e1 |
| e2 |
| e1 |
| e2 |
分析:(1)利用向量共线证明三点共线,先将
表示为
与
的和,再证明
=λ
,最后说明
,
有公共点B,即可证明A、B、D三点共线
(2)因为向量
,
的夹角为60°且|
|=|
|=1,所以
•
=
,故可将向量
,
作为基底,研究2
+
与向量
+k
垂直的问题,利用向量垂直的充要条件列方程即可得k值
| BD |
| BC |
| CD |
| BD |
| AB |
| AB |
| BD |
(2)因为向量
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| 1 |
| 2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
解答:解:(1)∵
=
+
,
=
+
=5
+5
∴
=5
即
,
共线,
∵
,
有公共点B
∴A,B,D三点共线.
(2)∵(2
+
)⊥(
+k
)
∴(2
+
)•(
+k
)=0
2
2+2k
+
+k
2=0
∵|
|=|
|=1,且
•
=|
|• |
|cos60°=
∴2+k+
+k=0
解得k=-
| AB |
| e1 |
| e2 |
| BD |
| BC |
| CD |
| e1 |
| e2 |
∴
| BD |
| AB |
| AB |
| BD |
∵
| AB |
| BD |
∴A,B,D三点共线.
(2)∵(2
| e1 |
| e2 |
| e1 |
| e2 |
∴(2
| e1 |
| e2 |
| e1 |
| e2 |
2
| e1 |
| e1 |
| e2 |
| e1 |
| e2 |
| e2 |
∵|
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| 1 |
| 2 |
∴2+k+
| 1 |
| 2 |
解得k=-
| 5 |
| 4 |
点评:本题考察了向量共线的充要条件,向量垂直的充要条件,向量数量积运算性质及应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设单位向量
,
的夹角为60°,则向量3
+4
与向量
的夹角的余弦值是( )
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
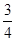 B.
B. C.
C. D.
D.