题目内容
给出下列命题:①存在实数α,使sinα•cosα=1;
②存在实数α,使
 ;
;③函数
 是偶函数;
是偶函数;④
 是函数
是函数 的一条对称轴方程;
的一条对称轴方程;⑤若α、β是第一象限的角,且α>β,则sinα>sinβ;
其中正确命题的序号是 .
【答案】分析:由二倍角的正弦公式结合正弦的最大值为1,可得①不正确;利用辅助角公式,可得sinα+cosα的最大值为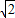 ,小于
,小于 ,故②不正确;用诱导公式进行化简,结合余弦函数是R上的偶函数,得到③正确;根据y=Asin(ωx+∅)图象对称轴的公式,可得④正确;通过举出反例,得到⑤不正确.由此得到正确答案.
,故②不正确;用诱导公式进行化简,结合余弦函数是R上的偶函数,得到③正确;根据y=Asin(ωx+∅)图象对称轴的公式,可得④正确;通过举出反例,得到⑤不正确.由此得到正确答案.
解答:解:对于①,因为sinα•cosα= sin2α
sin2α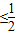 ,故不存在实数α,使sinα•cosα=1,所以①不正确;
,故不存在实数α,使sinα•cosα=1,所以①不正确;
对于②,因为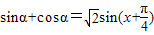 ≤
≤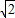 ,而
,而
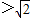 ,
,
说明不存在实数α,使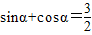 ,所以②不正确;
,所以②不正确;
对于③,因为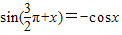 ,而cosx是偶函数,所以函数
,而cosx是偶函数,所以函数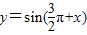 是偶函数,故③正确;
是偶函数,故③正确;
对于④,当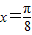 时,函数
时,函数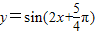 的值为
的值为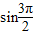 =-1为最小值,
=-1为最小值,
故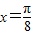 是函数
是函数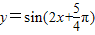 的一条对称轴方程,④正确;
的一条对称轴方程,④正确;
对于⑤,当α=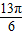 、β=
、β=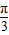 时,都是第一象限的角,且α>β,
时,都是第一象限的角,且α>β,
但sinα= <
<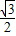 =sinβ,故⑤不正确.
=sinβ,故⑤不正确.
故答案为:③④
点评:本题以命题真假的判断为载体,考查了二倍角的正弦公式、三角函数的奇偶性和图象的对称轴等知识,属于中档题.
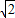 ,小于
,小于 ,故②不正确;用诱导公式进行化简,结合余弦函数是R上的偶函数,得到③正确;根据y=Asin(ωx+∅)图象对称轴的公式,可得④正确;通过举出反例,得到⑤不正确.由此得到正确答案.
,故②不正确;用诱导公式进行化简,结合余弦函数是R上的偶函数,得到③正确;根据y=Asin(ωx+∅)图象对称轴的公式,可得④正确;通过举出反例,得到⑤不正确.由此得到正确答案.解答:解:对于①,因为sinα•cosα=
 sin2α
sin2α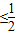 ,故不存在实数α,使sinα•cosα=1,所以①不正确;
,故不存在实数α,使sinα•cosα=1,所以①不正确;对于②,因为
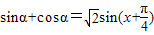 ≤
≤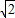 ,而
,而
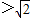 ,
,说明不存在实数α,使
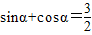 ,所以②不正确;
,所以②不正确;对于③,因为
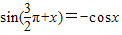 ,而cosx是偶函数,所以函数
,而cosx是偶函数,所以函数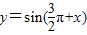 是偶函数,故③正确;
是偶函数,故③正确;对于④,当
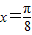 时,函数
时,函数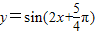 的值为
的值为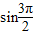 =-1为最小值,
=-1为最小值,故
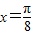 是函数
是函数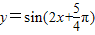 的一条对称轴方程,④正确;
的一条对称轴方程,④正确;对于⑤,当α=
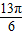 、β=
、β=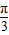 时,都是第一象限的角,且α>β,
时,都是第一象限的角,且α>β,但sinα=
 <
<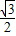 =sinβ,故⑤不正确.
=sinβ,故⑤不正确.故答案为:③④
点评:本题以命题真假的判断为载体,考查了二倍角的正弦公式、三角函数的奇偶性和图象的对称轴等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目