题目内容
若 和
和 是两个不共线的向量,则下面的四组向量中,共线的一组的是( )
是两个不共线的向量,则下面的四组向量中,共线的一组的是( )A.
 和
和 -
-
B.3
 -2
-2 和-6
和-6 +4
+4
C.
 +2
+2 和2
和2 +
+
D.
 +2
+2 和
和 +
+
【答案】分析:由 和
和 是两不共线的向量,根据共线向量定理知A,B,C,D选项中共线或不共线,求出结果.
是两不共线的向量,根据共线向量定理知A,B,C,D选项中共线或不共线,求出结果.
解答:解:在A中,∵ 和
和 是两不共线的向量,
是两不共线的向量,
∴ 和
和 -
- 不共线,
不共线,
在B中,∵2(3 -2
-2 )=-6
)=-6 +4
+4 ,
,
∴3 -2
-2 和-6
和-6 +4
+4 共线.
共线.
在C中,∵ 和
和 是两个不共线的向量
是两个不共线的向量
∴ +2
+2 和2
和2 +
+ 不共线,
不共线,
在D中,∵ 和
和 是两个不共线的向量
是两个不共线的向量
∴ +2
+2 和
和 +
+ 不共线,
不共线,
故选B.
点评:本题考查平行向量的性质和应用,是基础题.解题时要认真审题,正确解题的关键是知道共线的向量不能作为平面向量的一组基底.
 和
和 是两不共线的向量,根据共线向量定理知A,B,C,D选项中共线或不共线,求出结果.
是两不共线的向量,根据共线向量定理知A,B,C,D选项中共线或不共线,求出结果.解答:解:在A中,∵
 和
和 是两不共线的向量,
是两不共线的向量,∴
 和
和 -
- 不共线,
不共线,在B中,∵2(3
 -2
-2 )=-6
)=-6 +4
+4 ,
,∴3
 -2
-2 和-6
和-6 +4
+4 共线.
共线.在C中,∵
 和
和 是两个不共线的向量
是两个不共线的向量∴
 +2
+2 和2
和2 +
+ 不共线,
不共线,在D中,∵
 和
和 是两个不共线的向量
是两个不共线的向量∴
 +2
+2 和
和 +
+ 不共线,
不共线,故选B.
点评:本题考查平行向量的性质和应用,是基础题.解题时要认真审题,正确解题的关键是知道共线的向量不能作为平面向量的一组基底.

练习册系列答案
相关题目
 和
和 是两个不共线的向量,则下面的四组向量中,共线的一组的是( )
是两个不共线的向量,则下面的四组向量中,共线的一组的是( ) 和
和 是两个不共线的向量,则下面的四组向量中,共线的一组的是
是两个不共线的向量,则下面的四组向量中,共线的一组的是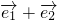 和
和 ,
, 是两个不共线的向量,已知
是两个不共线的向量,已知 =2
=2 +k
+k ,
, =
= +3
+3 ,
, =2
=2 -
- ,若A,B,D三点共线,则k= .
,若A,B,D三点共线,则k= . ,
, 是两个不共线的向量,已知
是两个不共线的向量,已知 =2
=2 +k
+k ,
, =
= +3
+3 ,
, =2
=2 -
- ,若A,B,D三点共线,则k= .
,若A,B,D三点共线,则k= .