题目内容
命题p:|x|<1,命题q: ,则
,则 是
是 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
解析试题分析:p真:-1<x<1,q真: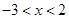 ,所以
,所以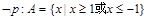 ,
,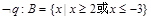 ,因为
,因为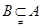 ,所以
,所以 是
是 成立的必要不充分条件.
成立的必要不充分条件.
考点:充要条件与简易逻辑的综合.
点评:要先求出p,q真的条件,得到 ,
, 真的条件,再根据
真的条件,再根据 ,
, 为真对应的集合之间的包含关系,从而可求出
为真对应的集合之间的包含关系,从而可求出 是
是 成立的充要关系.
成立的充要关系.

练习册系列答案
相关题目
“ ”是“
”是“ ”的 ( )
”的 ( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知 :函数
:函数 与
与 轴有两个交点;
轴有两个交点; :
: ,
, 恒成立.若
恒成立.若 为真,则实数m的取值范围为 ( )
为真,则实数m的取值范围为 ( )
A. | B. |
C. | D. |
“ ”是“函数
”是“函数 在其定义域上为奇函数”的( )
在其定义域上为奇函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题正确的是( )
A. | B. |
C. 是 是 的充分不必要条件 的充分不必要条件 | D.若 ,则 ,则 |
若命题“ 或
或 ”为真,“非p”为真,则( )
”为真,“非p”为真,则( )
| A.p真q真 | B.p假q真 | C.p真q假 | D.p假q假 |
已知命题 :
: ,
, ,那么下列结论正确的是( )
,那么下列结论正确的是( )
A. , , | B.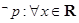 , , |
C. , , | D.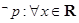 , , |
“a和b都不是偶数”的否定形式是
A. 和 和 至少有一个是偶数 至少有一个是偶数 | B. 和 和 至多有一个是偶数 至多有一个是偶数 |
C. 是偶数, 是偶数, 不是偶数 不是偶数 | D. 和 和 都是偶数 都是偶数 |
 ,则
,则 ”的否命题是“若
”的否命题是“若 ”
” :
: ,使
,使 ,则
,则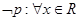 ,使
,使
 为假命题,则
为假命题,则 是函数
是函数 为偶函数的充要条件
为偶函数的充要条件