题目内容
已知⊙O是△ABC的外接圆,⊙I是△ABC的内切圆,∠A=80°,那么∠BOC=__________,∠BIC=__________.
思路点拨:由∠A的度数,易得∠BOC的度数,然后抓住圆的切线性质及三角形内角和可得到∠BIC的度数.
解:
如图,∵∠A=80°,由一条弧所对的圆周角等于它所对的圆心角的一半,得∠BOC=2∠A=160°,故第一个空应填160°.
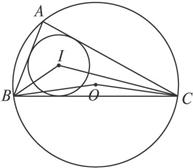
又∵在△ABC中,∠A=80°,
∴∠ABC+∠ACB=180°-80°=100°.
又∵∠IBC=![]() ∠ABC,∠ICB=
∠ABC,∠ICB=![]() ∠ACB,∴∠IBC+∠ICB=
∠ACB,∴∠IBC+∠ICB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×100°=50°.
×100°=50°.
∴在△IBC中,∠BIC=180°-50°=130°.
故第二个空填130°.
答案:
160° 130°
[一通百通]应用了三角形内切圆的有关定理,结合圆周角定理,构造三角形解题,是一道较好的客观题.

练习册系列答案
相关题目
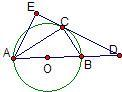 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB. 21、如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M,求证:PC是⊙O的切线.
21、如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M,求证:PC是⊙O的切线.