题目内容
已知O是△ABC的外心,若A(0,0),B(2,0),AC=1,∠BAC=
,且
=λ
+μ
,则λ+μ=
.
| 2π |
| 3 |
| AO |
| AB |
| AC |
| 13 |
| 6 |
| 13 |
| 6 |
分析:建立直角坐标系,求出三角形各顶点的坐标,因为O为△ABC的外心,把AB的中垂线 m方程和AC的中垂线 n的方程,联立方程组,求出O的坐标,利用已知向量间的关系,待定系数法求λ和μ 的值.
解答:解:如图:以A为原点,以AB所在的直线为x轴,建立直角系:
则A(0,0),B (2,0),C(-
,
),
∵O为△ABC的外心,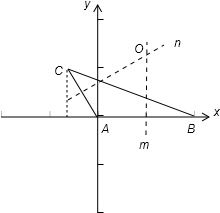
∴O在AB的中垂线 m:x=1 上,又在AC的中垂线 n 上,
AC的中点(-
,
),AC的斜率为-
,
∴中垂线n的方程为 y-
=
(x+
).
把直线 m和n 的方程联立方程组解得△ABC的外心O(1,
),
由条件
=λ
+μ
得
(1,
)=λ(2,0)+μ(-
,
)=(2λ-
μ,
μ),
∴2λ-
μ=1,
μ=
.
解得 λ=
,μ=
,∴λ+μ=
,
故答案为
.
则A(0,0),B (2,0),C(-
| 1 |
| 2 |
| ||
| 2 |
∵O为△ABC的外心,

∴O在AB的中垂线 m:x=1 上,又在AC的中垂线 n 上,
AC的中点(-
| 1 |
| 4 |
| ||
| 4 |
| 3 |
∴中垂线n的方程为 y-
| ||
| 4 |
| ||
| 3 |
| 1 |
| 4 |
把直线 m和n 的方程联立方程组解得△ABC的外心O(1,
2
| ||
| 3 |
由条件
| AO |
| AB |
| AC |
(1,
2
| ||
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴2λ-
| 1 |
| 2 |
| ||
| 2 |
2
| ||
| 3 |
解得 λ=
| 5 |
| 6 |
| 4 |
| 3 |
| 13 |
| 6 |
故答案为
| 13 |
| 6 |
点评:本题考查求两条直线的交点坐标的方法,三角形外心的性质,向量的坐标表示及向量相等的条件,待定系数法求参数值.属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目