题目内容

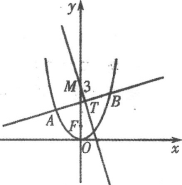
【题目】过点作一直线与双曲线相交于、两点，若为中点，则( )

A. B. C. D.

【答案】D

【解析】

设出直线AB的方程与双曲线方程联立消去y，设两实根为，，利用韦达定理可表示出的值，根据P点坐标求得＝8进而求得k，则直线AB的方程可得；利用弦长公式求得|AB|．

解：易知直线AB不与y轴平行，设其方程为y﹣2＝k（x﹣4）

代入双曲线C：，整理得（1﹣2k2）x2+8k（2k﹣1）x﹣32k2+32k﹣10＝0

设此方程两实根为，，则

又P（4，2）为AB的中点，

所以8，

解得k＝1

当k＝1时，直线与双曲线相交，即上述二次方程的△＞0，

所求直线AB的方程为y﹣2＝x﹣4化成一般式为x﹣y﹣2＝0．＝8，＝10

|AB|||4．

故选：D．

练习册系列答案
相关题目

【题目】已知数列是首项为1，公差为的等差数列，数列是首项为1，公比为的等比数列．

（1）若，求数列的前项和；

（2）若存在正整数，使得，试比较与的大小，并说明理由．

【题目】已知顶点在原点，焦点在轴上的抛物线过点.

（1）求抛物线的标准方程；

（2）斜率为的直线与抛物线交于、两点，点是线段的中点，求直线的方程，并求线段的长.

【题目】设D是圆O：x2+y2＝16上的任意一点，m是过点D且与x轴垂直的直线，E是直线m与x轴的交点，点Q在直线m上，且满足2|EQ||ED|．当点D在圆O上运动时，记点Q的轨迹为曲线C．

（1）求曲线C的方程．

（2）已知点P（2，3），过F（2，0）的直线l交曲线C于A，B两点，交直线x＝8于点M．判定直线PA，PM，PB的斜率是否依次构成等差数列？并说明理由．

【题目】在平面直角坐标系xOy中，已知曲线C1：（t为参数），C2：（m为参数）．

（1）将C1，C2的方程化为普通方程，并说明它们分别表示什么曲线；

（2）设曲线C1与C2的交点分别为A，B，O为坐标原点，求△OAB的面积的最小值．

【题目】十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求，带领广大农村地区人民群众脱贫奔小康。经过不懈的奋力拼搏，新农村建设取得巨大进步，农民年收入也逐年增加。为了更好的制定2019年关于加快提升农民年收人力争早日脱贫的工作计划，该地扶贫办统计了2018年50位农民的年收人并制成如下频率分布直方图：

（1）根据频率分布直方图，估计50位农民的年平均收入（单位：千元）（同一组数据用该组数据区间的中点值表示）；

（2）由频率分布直方图，可以认为该贫困地区农民年收入服从正态分布，其中近似为年平均收入,近似为样本方差，经计算得.利用该正态分布，求:

(i)在2019年脱贫攻坚工作中，若使该地区约有占总农民人数的的农民的年收入高于扶贫办制定的最低年收入标准，则最低年收入大约为多少千元？

（ii）为了调研“精准扶贫，不落一人”的政策要求落实情况, 扶贫办随机走访了1000位农民。若每个农民的年收人相互独立，问：这1000位农民中的年收入不少于12.14千元的人数最有可能是多少？

附：参考数据与公式，若～，则①；②；③.

【题目】在无穷数列中，是给定的正整数，，．

（Ⅰ）若，写出的值；

（Ⅱ）证明：数列中存在值为的项；

（Ⅲ）证明：若互质，则数列中必有无穷多项为．

【题目】如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，侧棱AA1⊥底面ABCD，E为棱AA1的中点，AB=2，AA1=3．

（Ⅰ）求证：A1C∥平面BDE；

（Ⅱ）求证：BD⊥A1C；

（Ⅲ）求三棱锥A-BDE的体积．

【题目】已知抛物线C：x2＝4y的焦点为F，直线：y＝kx＋b（k≠0）交抛物线C于A、B两点，|AF|＋|BF|＝4，M（0，3）．

（1）若AB的中点为T，直线MT的斜率为，证明：k· 为定值；

（2）求△ABM面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网