题目内容

【题目】已知函数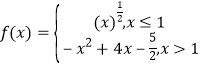，若函数的图象与轴的交点个数不少于2个，则实数的取值范围为（ ）

A. B.

C. D.

【答案】A

【解析】由题可知函数的图象与轴的交点个数不少于2个，即为函数y=f(x)的图像与函数y=mx+m的图像的交点个数不少于2个，由于函数y=mx+m的图像过定点P（-1,0），且斜率为m,作出函数y=f(x)的图像如图所示，

数形结合可知，当动直线过点A时有2个交点，当动直线为的切线时，即过点B时有两个交点，在这两种极限位置之间有3个交点，易知设直线y=mx+m与函数的图像相切，联立方程组由题可知又x>1.所以

过点（-1,0）作的切线，设切点坐标为，则此时，切线的斜率为

故实数m的取值范围为.综上实数m的取值范围为.

故选A.

练习册系列答案
相关题目

【题目】

在平面直角坐标系中，直线的参数方程为（为参数， 为直线的倾斜角，且），以原点为极点， 轴的正半轴为极轴建立极坐标系，圆的极坐标方程为.

（1）若直线经过圆的圆心，求直线的倾斜角；

（2）若直线与圆交于， 两点，且，点，求的取值范围.

【题目】已知命题甲成立，可推出命题乙不成立，则下列说法中，一定正确的是( )

A.命题甲不成立，可推出命题乙成立B.命题甲不成立，可推出命题乙不成立

C.命题乙成立，可推出命题甲成立D.命题乙成立，可推出命题甲不成立

【题目】已知动圆C过定点F（2，0），且与直线x=-2相切，圆心C的轨迹为E，

（1）求圆心C的轨迹E的方程；

（2）若直线l交E与P，Q两点，且线段PQ的中心点坐标（1，1），求|PQ|．

【题目】下列是关于复数的类比推理：

①复数的加减法运算可以类比多项式的加减法运算法则；

②由实数绝对值的性质|x|2=x2类比得到复数z的性质|z|2=z2；

③已知a，b∈R，若a－b>0，则a>b类比得已知z1，z2∈C，若z1－z2>0，则z1>z2；

④由向量加法的几何意义可以类比得到复数加法的几何意义.

其中推理结论正确的是__________.

【题目】若函数具备以下两个条件：（1）至少有一条对称轴或一个对称中心；（2）至少有两个零点，则称这样的函数为“多元素”函数，下列函数中为“多元素”函数的是_______.

①；②；③；④.

【题目】下列判断正确的是( )

A. 设是实数,则“”是“ ”的充分而不必要条件

B. :“,”则有:不存在,

C. 命题“若,则”的否命题为:“若,则”

D. “,”为真命题

【题目】已知函数．

（1）求的单调区间；

（2）求的最大值和最小值．

【题目】某中学随机选取了名男生，将他们的身高作为样本进行统计，得到如图所示的频率分布直方图．观察图中数据，完成下列问题．

（Ⅰ）求的值及样本中男生身高在（单位: ）的人数；

（Ⅱ）假设同一组中的每个数据可用该组区间的中点值代替，通过样本估计该校全体男生的平均身高；

（Ⅲ）在样本中，从身高在和（单位: ）内的男生中任选两人，求这两人的身高都不低于的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网