题目内容
一个空间几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C.40 | D.80 |
A
解析试题分析:由三视图知,几何体是一个四棱锥,四棱锥的底面是一个直角梯形,直角梯形的上底是1,下底是4,垂直于底边的腰是4,一条侧棱与底面垂直,这条侧棱长是4,∴四棱锥的体积是  ,故答案为:
,故答案为: .
.
考点:由三视图求面积、体积.

练习册系列答案
相关题目
要做一个圆锥形的漏斗,其母线长为10,要使其体积最大,则高应为( )
A. | B. | C. | D. |
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
| A.92+14π | B.82+14π |
| C.92+24π | D.82+24π |
某几何体的三视图如图所示,则该几何体的体积为( ).
| A.16+8π | B.8+8π | C.16+16π | D.8+16π |
一个几何体的三视图(侧视图中的弧线是半圆)如图所示,则该几何体的表面积是( ).
| A.20+4π | B.24+4π | C.20+3π | D.24+3π |
某几何体的三视图如图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为( ).
A.16+6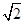 +4π cm2 +4π cm2 | B.16+6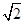 +3π cm2 +3π cm2 |
C.10+6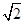 +4π cm2 +4π cm2 | D.10+6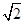 +3π cm2 +3π cm2 |
 的扇形,则该几何体的体积为( )
的扇形,则该几何体的体积为( )





