题目内容
要做一个圆锥形的漏斗，其母线长为10，要使其体积最大，则高应为( )
A． | B． | C． | D． |
B
解析试题分析：假设圆锥的高为
，所以底面半径
.所以圆锥的体积表达式为
.即
.所以由体积对高求导可得
.所以
，所以
.故选B.
考点：1.圆锥的体积公式.2.最值的求法.3.实际问题考虑定义域.
练习册系列答案
全优点练单元计划系列答案
相关题目
棱长为2的正方体
的内切球的表面积为（ ）
A． | B． | C． | D． |
一个空间几何体的三视图如图所示，则该几何体的体积为( )
A． | B． | C．40 | D．80 |
某几何体的三视图如图所示，则它的体积等于（ ）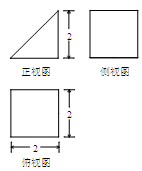
A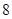． | B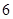． | C． | D． |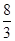
一个几何体的三视图如图所示，则该几何体可以是（ ）
| A．圆台 | B．棱台 | C．圆柱 | D．棱柱 |
圆柱的底面积为S,侧面展开图为正方形,那么这个圆柱的侧面积为( )
A． | B． | C． | D． |
下列判断正确的是（ ）
| A．棱柱中只能有两个面可以互相平行 | B．底面是正方形的直四棱柱是正四棱柱 |
| C．底面是正六边形的棱台是正六棱台 | D．底面是正方形的四棱锥是正四棱锥 |
下图是某几何体的三视图，则该几何体的体积为（ ）
A． | B． | C． | D． |
一个几何体的三视图如图所示，且其侧视图是一个等边三角形，则这个几何体的体积为( )．
A．12＋ | B．36＋ | C．18＋ | D．6＋ |