Question

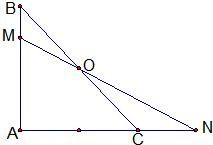如图在等腰直角△ABC中，点O是斜边BC的中点，过点O的直线分别交直线AB、AC于不同的两点M、N，若

AB

=m

AM，

AC

=n

AN

，则mn的最大值为（　　）

• A、

  1

  2

• B、1
• C、2
• D、3

Answer 1

分析：利用三角形的直角建立坐标系，求出各个点的坐标，有条件求出M和N坐标，则由截距式直线方程求出MN的直线方程，根据点
O（1，1）在直线上，求出m和n的关系式，利用基本不等式求出mn的最大值，注意成立时条件是否成立．

解答：解：以AC、AB为x、y轴建立直角坐标系，设等腰直角△ABC的腰长为2，
则O点坐标为（1，1），B（0，2）、C（2，0），
∵

AB

=m

AM，

AC

=n

AN

，
∴

AM

=

AB

m

，

AN

=

AC

n

，
∴M(0，

2

m

)、N(

2

n

，0)，
∴直线MN的方程为

nx

2

+

my

2

=1，
∵直线MN过点O（1，1），
∴

m

2

+

n

2

=1，即m+n=2
∵m+n≥2

mn

（m＞0，n＞0），
∴mn≤

(m+n)2

4

=1，
∴当且仅当m=n=1时取等号，且mn的最大值为1．
故选B．

点评：本题的考查了利用向量的坐标运算求最值问题，需要根据图形的特征建立坐标系，转化为几何问题，根据条件求出两数的和，再由基本不等式求出它们的积的最大值，注意验证三个条件：一正二定三相等，考查了转化思想．