题目内容
如图在等腰直角△ABC中,点O是斜边BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若
=m
=n
,则mn的最大值为( )

| AB |
| AM, |
| AC |
| AN |
A.
| B.1 | C.2 | D.3 |

以AC、AB为x、y轴建立直角坐标系,设等腰直角△ABC的腰长为2,
则O点坐标为(1,1),B(0,2)、C(2,0),
∵
=m
=n
,
∴
=
,
=
,
∴M(0,
)、N(
,0),
∴直线MN的方程为
+
=1,
∵直线MN过点O(1,1),
∴
+
=1,即m+n=2
∵m+n≥2
(m>0,n>0),
∴mn≤
=1,
∴当且仅当m=n=1时取等号,且mn的最大值为1.
故选B.
则O点坐标为(1,1),B(0,2)、C(2,0),
∵
| AB |
| AM, |
| AC |
| AN |
∴
| AM |
| ||
| m |
| AN |
| ||
| n |
∴M(0,
| 2 |
| m |
| 2 |
| n |
∴直线MN的方程为
| nx |
| 2 |
| my |
| 2 |
∵直线MN过点O(1,1),
∴
| m |
| 2 |
| n |
| 2 |
∵m+n≥2
| mn |
∴mn≤
| (m+n)2 |
| 4 |
∴当且仅当m=n=1时取等号,且mn的最大值为1.
故选B.

练习册系列答案
相关题目
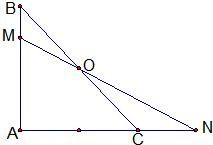 如图在等腰直角△ABC中,点O是斜边BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若
如图在等腰直角△ABC中,点O是斜边BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若
 ,则mn的最大值为( )
,则mn的最大值为( )

 ,则mn的最大值为( )
,则mn的最大值为( )
