Question

17．如图，网格纸上正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（　　）

• A． 3$\sqrt{2}$
• B． 3$\sqrt{3}$
• C． 4$\sqrt{2}$
• D． 4$\sqrt{3}$

Answer 1

分析 由多面体的三视图得到该多面体是如图所示的四棱锥S-ABCD，其中底面ABCD是边长为3的正方形，SD⊥底面ABCD，且SD=3，由此能求出最长的棱的长度．

解答 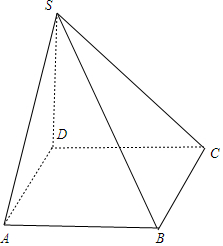解：由多面体的三视图得到该多面体是如图所示的四棱锥S-ABCD，
其中底面ABCD是边长为3的正方形，SD⊥底面ABCD，且SD=3，
∴最长的棱为SB，
∴最长的棱的长度SB=$\sqrt{B{D}^{2}+S{D}^{2}}$=$\sqrt{{3}^{2}+{3}^{2}+{3}^{2}}$=3$\sqrt{3}$．
故选：B．

点评 本题考查多面体的最长棱的长度的求法，考查三视图、四棱锥等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想，是基础题．