Question

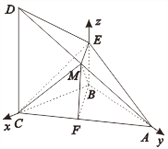
【题目】已知四棱锥A-BCDE中，底面BCDE为直角梯形，CD⊥平面ABC，侧面ABC是等腰直角三角形，∠EBC=∠ABC=90°，BC=CD=2BE=2，点M是棱AD的中点

(I)证明:平面AED⊥平面ACD;

(Ⅱ)求锐二面角B-CM-A的余弦值

Answer 1

【答案】(Ⅰ)证明见解析；(Ⅱ) .

【解析】试题分析：（1）平面ACD，又EM//BF，所以平面ACD，所以平面平面；（2）建立空间直角坐标系，求得两个法向量,，求出二面角。

试题解析：

（I）证明：取AC的中点F，连接BF，

因为AB＝BC，所以， 平面ABC,所以CD .

又所以平面ACD.①

因为AM=MD，AF=CF，所以.

因为 ，所以//MF，

所以四边形BFME是平行四边形.所以EM//BF.②

由①②,得平面ACD，所以平面平面；

（II）BE平面ABC，

又，

以点B为原点，直线BC、BA、BE分别为x,y,z轴，

建立空间直角坐标系B-xyz.

由，得B(0,0,0)，C(2,0,0)，A(0,2,0)，D(2,0,2).

由中点坐标公式得， ,，

设向量为平面BMC的一个法向量，则即

令y=1,得x=0，z=－1，即,

由（I）知， 是平面ACD的一个法向量.

设二面角B－CM－A的平面角为，

则，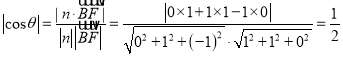

又二面角B－CM－A为锐二面角，故.