题目内容
某品牌专卖店准备在春节期间举行促销活动,根据市场调查,该店决定从2种型号的洗衣机,2种型号的电视机和3种型号的电脑中,选出3种型号的商品进行促销.(Ⅰ)试求选出的3种型号的商品中至少有一种是电脑的概率;
(Ⅱ)该店对选出的商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得m元奖金.假设顾客每次抽奖时获奖与否的概率都是
| 1 | 2 |
(Ⅲ)在(Ⅱ)的条件下,问该店若想采用此促销方案获利,则每次中奖奖金要低于多少元?
分析:(Ⅰ)由题意知本题是一个古典概型,从2种型号的洗衣机,2种型号的电视机,3种型号的电脑中,选出3种型号的商品一共C73种选法.选出的3种型号的商品中没有电脑的选法有C43种,根据古典概型公式得到结果.
(2)X的所有可能的取值为0,m,2m,3m.当X=0时表示顾客在三次抽奖中都没有中奖,由独立重复试验的公式得到概率,同理对于其他的变量的值,用同样方法做出.
(3)要使促销方案对商场有利,应使顾客获奖奖金总额的数学期望低于商场的提价数额,因此应有1.5m<150,根据列出的不等式得到变量m的范围.
(2)X的所有可能的取值为0,m,2m,3m.当X=0时表示顾客在三次抽奖中都没有中奖,由独立重复试验的公式得到概率,同理对于其他的变量的值,用同样方法做出.
(3)要使促销方案对商场有利,应使顾客获奖奖金总额的数学期望低于商场的提价数额,因此应有1.5m<150,根据列出的不等式得到变量m的范围.
解答:解:(Ⅰ)由题意知本题是一个古典概型,
∵从2种型号的洗衣机,2种型号的电视机,3种型号的电脑中,
选出3种型号的商品一共C73种选法.
选出的3种型号的商品中没有电脑的选法有C43种,
∴选出的3种型号的商品中至少有一种是电脑的概率为P=1-
=
.
(Ⅱ)X的所有可能的取值为0,m,2m,3m.
X=0时表示顾客在三次抽奖中都没有中奖,
∴P(X=0)=
(
)0(
)3=
同理可得
P(X=m)=C31(
)1(
)2=
,
P(X=2m)=
(
)2(
)1=
P(X=3m)=C33(
)3(
)0=
∴顾客在三次抽奖中所获得的奖金总额X的分布列为:
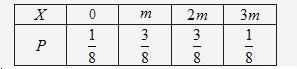
于是顾客在三次抽奖中所获得的奖金总额的数学期望是
EX=0×
+m×
+2m×
+3m×
=1.5m
(Ⅲ)要使促销方案对商场有利,应使顾客获奖奖金总额的数学期望低于商场的提价数额,
因此应有1.5m<150,所以m<100.
故每次中奖奖金要低于100元,才能使促销方案对商场有利.
∵从2种型号的洗衣机,2种型号的电视机,3种型号的电脑中,
选出3种型号的商品一共C73种选法.
选出的3种型号的商品中没有电脑的选法有C43种,
∴选出的3种型号的商品中至少有一种是电脑的概率为P=1-
| ||
|
| 31 |
| 35 |
(Ⅱ)X的所有可能的取值为0,m,2m,3m.
X=0时表示顾客在三次抽奖中都没有中奖,
∴P(X=0)=
| C | 0 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
同理可得
P(X=m)=C31(
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
P(X=2m)=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
P(X=3m)=C33(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
∴顾客在三次抽奖中所获得的奖金总额X的分布列为:

于是顾客在三次抽奖中所获得的奖金总额的数学期望是
EX=0×
| 1 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 1 |
| 8 |
(Ⅲ)要使促销方案对商场有利,应使顾客获奖奖金总额的数学期望低于商场的提价数额,
因此应有1.5m<150,所以m<100.
故每次中奖奖金要低于100元,才能使促销方案对商场有利.
点评:本题与我们生活关系密切,本题可以培养学生运用数学思想,提高发现问题、分析问题、解决问题的能力,增强学生数学思维情趣,形成学习数学知识的积极态度.

练习册系列答案
相关题目
 元奖金.假设顾客每次抽奖时获奖与否的概率都是
元奖金.假设顾客每次抽奖时获奖与否的概率都是 ,
, 元的概率;
元的概率; .请写出
.请写出 ,设顾客在三次抽奖中所获得的奖金总额(单位:元)为随机变量X.
,设顾客在三次抽奖中所获得的奖金总额(单位:元)为随机变量X.