题目内容
在四个函数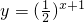 ,y=2x+1,y=2x-1,y=lgx中同时满足:①对任意的x,y∈R,f(x+y)=2f(x)•f(y)和 ②
,y=2x+1,y=2x-1,y=lgx中同时满足:①对任意的x,y∈R,f(x+y)=2f(x)•f(y)和 ②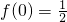 .
.
的函数为________(写出一个函数即可)
y=2x-1
分析:由题意,利用所给的两个条件,对四个函数进行验证,排除不符合题意的,即可找出符合条件的函数,由于条件②较简单,故可用它先筛选,然后再用第一个条件筛选出符合条件的函数
解答:考察题设,条件②较简单,可先用它排除不符合条件的函数,易知,可排除y=2x+1,y=lgx
对于函数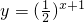 ,f(x+y)=
,f(x+y)=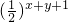 =2×
=2×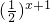 ×
×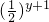 =2f(x)•f(y),此函数符合题意
=2f(x)•f(y),此函数符合题意
对于函数y=2x-1,f(x+y)=2x+y-1=2×2x-1×2y-1=2f(x)•f(y),此函数符合题意
综上,两个函数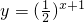 与y=2x-1都符合题意,根据题设条件要求选其一即可
与y=2x-1都符合题意,根据题设条件要求选其一即可
故答案为y=2x-1
点评:本题考查指数函数的解析式及运算规则,对数函数的定义域,解答本题的关键是理解指数幂的运算性质,理解题设中所给的两个条件,本题考查的重点是指数幂的运算,属于指数计算题
分析:由题意,利用所给的两个条件,对四个函数进行验证,排除不符合题意的,即可找出符合条件的函数,由于条件②较简单,故可用它先筛选,然后再用第一个条件筛选出符合条件的函数
解答:考察题设,条件②较简单,可先用它排除不符合条件的函数,易知,可排除y=2x+1,y=lgx
对于函数
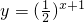 ,f(x+y)=
,f(x+y)=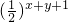 =2×
=2×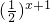 ×
×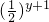 =2f(x)•f(y),此函数符合题意
=2f(x)•f(y),此函数符合题意对于函数y=2x-1,f(x+y)=2x+y-1=2×2x-1×2y-1=2f(x)•f(y),此函数符合题意
综上,两个函数
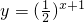 与y=2x-1都符合题意,根据题设条件要求选其一即可
与y=2x-1都符合题意,根据题设条件要求选其一即可故答案为y=2x-1
点评:本题考查指数函数的解析式及运算规则,对数函数的定义域,解答本题的关键是理解指数幂的运算性质,理解题设中所给的两个条件,本题考查的重点是指数幂的运算,属于指数计算题

练习册系列答案
相关题目
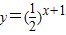 ,y=2x+1,y=2x-1,y=lgx中同时满足:①对任意的x,y∈R,f(x+y)=2f(x)•f(y)和 ②
,y=2x+1,y=2x-1,y=lgx中同时满足:①对任意的x,y∈R,f(x+y)=2f(x)•f(y)和 ②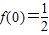 .
.