题目内容
(本小题满分13分)在等比数列 中,
中, .
.
(1)求等比数列 的通项公式;
的通项公式;
(2)若等差数列 中,
中, ,求等差数列
,求等差数列 的前
的前 项的和
项的和 ,并求
,并求 的最大值.
的最大值.
(1) ; (2)
; (2) ,当
,当 时,
时, 最大值为72.
最大值为72.
【解析】
试题分析:(1)在等比数列 中,设公比为
中,设公比为 ,然后由题设列方程求出
,然后由题设列方程求出 和
和  ,从而得到数列的通项公式;
,从而得到数列的通项公式;
(2)在等差数列 中,设公差为
中,设公差为 ,然后由题设列方程求出
,然后由题设列方程求出 和
和 ,再由等差数列的前
,再由等差数列的前 项和公式求出
项和公式求出 ,并结合二次函数确定
,并结合二次函数确定 的最大值.
的最大值.
试题解析:【解析】
(1)在等比数列 中,设公比为
中,设公比为 ,
,
因为  ,
,
所以  得
得
所以数列 的通项公式是
的通项公式是  . 5分
. 5分
(2)在等差数列 中,设公差为
中,设公差为 .
.
因为  ,
,
所以 

 9分
9分
方法一
 ,
,
当 时,
时, 最大值为72. 13分
最大值为72. 13分
方法二
由 ,当
,当 ,解得
,解得 ,即
,即
所以当 时,
时, 最大值为72. 13分
最大值为72. 13分
考点:1、等差数列;2、等比数列.

练习册系列答案
相关题目
 (
( ),若无论
),若无论 为何值,函数
为何值,函数 的图象总是一条直线,则
的图象总是一条直线,则 的值是______.
的值是______.
 B.
B. C.
C. D.
D.
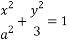 的右焦点为F,直线
的右焦点为F,直线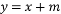 与椭圆E交于A,B两点.若△EAB周长的最大值是8,则m的值等于 ( ).
与椭圆E交于A,B两点.若△EAB周长的最大值是8,则m的值等于 ( ). D. 2
D. 2 则
则 是( ).
是( ). B.
B.
 D.
D.
 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= . “
“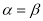 ”是“
”是“ ”的
”的 的解,下列判断不正确的是 ( )
的解,下列判断不正确的是 ( ) 时,无解 B.
时,无解 B. 时,2个解
时,2个解 
 时,4个解 D.
时,4个解 D.
 时,无解
时,无解