题目内容
已知锐角三角形ABC中内角A、B、C的对边分别为a,b,c,a2+b2=6abcosC,且sin2C=2sinAsinB.
(1)求角C的值;
(2)设函数 ,且f(x)图象上相邻两最高点间的距离为π,求f(A)的取值范围.
,且f(x)图象上相邻两最高点间的距离为π,求f(A)的取值范围.
解:(1)∵sin2C=2sinAsinB,∴由正弦定理有:c2=2ab,
由余弦定理有:a2+b2=c2+2abcosC=c2(1+cosC)①
又a2+b2=6abcosC=3c2cosC②
由①②得1+cosC=3cosC,∴cosC= ,
,
又0<C<π,∴C= ;
;
(2) =
= sin(ωx-
sin(ωx- )
)
∵f(x)图象上相邻两最高点间的距离为π,
∴T=π
∴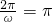
∴ω=2
∴f(x)= sin(2x-
sin(2x- )
)
∴f(A)= sin(2A-
sin(2A- )
)
∵ <A<
<A< ,∴0<2A-
,∴0<2A- <
<
∴0<sin(2A- )≤1
)≤1
∴0<f(A)≤ .
.
分析:(1)利用正弦定理与余弦定理可求得cosC的值,即可求得C的值;
(2)化简函数,利用周期确定ω,进而可得函数的解析式,即可求f(A)的取值范围.
点评:本题考查正弦定理与余弦定理,考查三角函数的图象与性质,考查学生的计算能力,属于中档题.
由余弦定理有:a2+b2=c2+2abcosC=c2(1+cosC)①
又a2+b2=6abcosC=3c2cosC②
由①②得1+cosC=3cosC,∴cosC=
 ,
,又0<C<π,∴C=
 ;
;(2)
 =
= sin(ωx-
sin(ωx- )
)∵f(x)图象上相邻两最高点间的距离为π,
∴T=π
∴
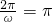
∴ω=2
∴f(x)=
 sin(2x-
sin(2x- )
)∴f(A)=
 sin(2A-
sin(2A- )
)∵
 <A<
<A< ,∴0<2A-
,∴0<2A- <
<
∴0<sin(2A-
 )≤1
)≤1∴0<f(A)≤
 .
.分析:(1)利用正弦定理与余弦定理可求得cosC的值,即可求得C的值;
(2)化简函数,利用周期确定ω,进而可得函数的解析式,即可求f(A)的取值范围.
点评:本题考查正弦定理与余弦定理,考查三角函数的图象与性质,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目