题目内容
长方体ABCD-A1B1C1D1中,AB=3,AD=2,AA1=1,则从A点沿表面到C1点的最短距离为
3
| 2 |
3
.| 2 |
分析:根据题意,画出三种展开的图形,求出A、C1两点间的距离,比较大小,从而找出最小值即为所求.
解答: 解:长方体ABCD-A1B1C1D1的表面可如下图三种方法展开后,A、C1两点间的距离分别为:
解:长方体ABCD-A1B1C1D1的表面可如下图三种方法展开后,A、C1两点间的距离分别为:
=3
,
=2
,
=
.
三者比较得3
是从点A沿表面到C1的最短距离,
∴最短距离是3
.
故答案为:3
.
 解:长方体ABCD-A1B1C1D1的表面可如下图三种方法展开后,A、C1两点间的距离分别为:
解:长方体ABCD-A1B1C1D1的表面可如下图三种方法展开后,A、C1两点间的距离分别为:| (1+2)2+32 |
| 2 |
| (3+1)2+22 |
| 5 |
| (3+2)2+12 |
| 26 |
三者比较得3
| 2 |
∴最短距离是3
| 2 |
故答案为:3
| 2 |
点评:本题考查棱柱的结构特征,考查分类讨论思想,考查计算能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
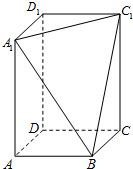 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.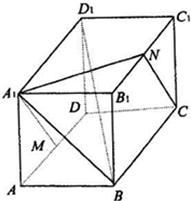 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.