题目内容
设函数f(x)=sin(ωx+φ)+cos(ωx+φ)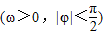 的最小正周期为π,且f(-x)=f(x),则( )
的最小正周期为π,且f(-x)=f(x),则( )A.f(x)在
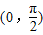 单调递减
单调递减B.f(x)在(
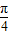 ,
,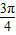 )单调递减
)单调递减C.f(x)在(0,
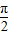 )单调递增
)单调递增D.f(x)在(
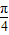 ,
,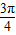 )单调递增
)单调递增
【答案】分析:利用辅助角公式将函数表达式进行化简,根据周期与ω的关系确定出ω的值,根据函数的偶函数性质确定出φ的值,再对各个选项进行考查筛选.
解答:解:由于f(x)=sin(ωx+ϕ)+cos(ωx+ϕ)=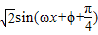 ,由于该函数的最小正周期为π=
,由于该函数的最小正周期为π=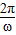 ,得出ω=2,又根据f(-x)=f(x),以及|φ|<
,得出ω=2,又根据f(-x)=f(x),以及|φ|<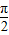 ,得出φ=
,得出φ=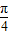 .因此,f(x)=
.因此,f(x)=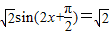 cos2x,若x∈
cos2x,若x∈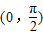 ,则2x∈(0,π),从而f(x)在
,则2x∈(0,π),从而f(x)在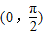 单调递减,若x∈(
单调递减,若x∈(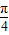 ,
,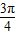 ),则2x∈(
),则2x∈(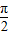 ,
,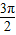 ),该区间不为余弦函数的单调区间,故B,C,D都错,A正确.
),该区间不为余弦函数的单调区间,故B,C,D都错,A正确.
故选A.
点评:本题考查三角函数解析式的确定问题,考查辅助角公式的运用,考查三角恒等变换公式的逆用等问题,考查学生分析问题解决问题的能力和意识,考查学生的整体思想和余弦曲线的认识和把握.属于三角中的基本题型.
解答:解:由于f(x)=sin(ωx+ϕ)+cos(ωx+ϕ)=
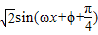 ,由于该函数的最小正周期为π=
,由于该函数的最小正周期为π=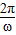 ,得出ω=2,又根据f(-x)=f(x),以及|φ|<
,得出ω=2,又根据f(-x)=f(x),以及|φ|<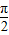 ,得出φ=
,得出φ=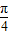 .因此,f(x)=
.因此,f(x)=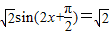 cos2x,若x∈
cos2x,若x∈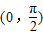 ,则2x∈(0,π),从而f(x)在
,则2x∈(0,π),从而f(x)在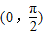 单调递减,若x∈(
单调递减,若x∈(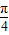 ,
,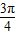 ),则2x∈(
),则2x∈(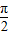 ,
,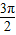 ),该区间不为余弦函数的单调区间,故B,C,D都错,A正确.
),该区间不为余弦函数的单调区间,故B,C,D都错,A正确.故选A.
点评:本题考查三角函数解析式的确定问题,考查辅助角公式的运用,考查三角恒等变换公式的逆用等问题,考查学生分析问题解决问题的能力和意识,考查学生的整体思想和余弦曲线的认识和把握.属于三角中的基本题型.

练习册系列答案
相关题目