题目内容
已知a,b,c均为正数,且a+b>c,求证: 。
。
 。
。 证明:设 ,
,
设0<x1<x2,
则f(x1)-f(x2)= ,
,
∴f(x1)<f(x2),
∴f(x)在(0,+∞)上单调递增,
∵a+b>c,
∴f(a+b)>f(c),
即 ,
,
又f(a)+f(b)= ,
,
∴ 。
。
 ,
,设0<x1<x2,
则f(x1)-f(x2)=
 ,
,∴f(x1)<f(x2),
∴f(x)在(0,+∞)上单调递增,
∵a+b>c,
∴f(a+b)>f(c),
即
 ,
,又f(a)+f(b)=
 ,
,∴
 。
。 
练习册系列答案
相关题目
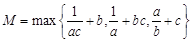 ,则M的最小值为 .
,则M的最小值为 .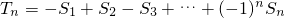 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;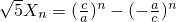 (n∈N+),证明:数列{
(n∈N+),证明:数列{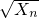 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.