Question

【题目】椭圆+=1与双曲线-=1有公共的焦点F1，F2，P是两曲线的一个交点，则cos∠F1PF2=______ ．

Answer 1

【答案】

【解析】

不妨设点P在第一象限，再根据椭圆、双曲线的定义和性质，可得|PF1|+|PF2|=2，|PF1|-|PF2|=2，求得|PF1|和|PF2|的值，根据|F1F2|=4，利用余弦定理可得cos∠F1PF2的值．

由题意设焦点F2（2，0）、F1（-2，0），∴3+b2=4，求得b2=1，

双曲线-=1，即双曲线-y2=1．

不妨设点P在第一象限，

再根据椭圆、双曲线的定义和性质，可得|PF1|+|PF2|=2，|PF1|-|PF2|=2，

可得|PF1|=+，|PF2|=-，且|F1F2|=4．

再由余弦定理可得cos∠F1PF2=

即=，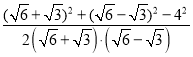

故答案为：．