题目内容
空间四边形OABC中,OB=OC,AOB=AOC=600,则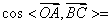 ( )
( )
A. B.
B.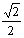 C.
C. D.0
D.0
D

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
题目内容
空间四边形OABC中,OB=OC,AOB=AOC=600,则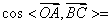 ( )
( )
A. B.
B.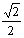 C.
C. D.0
D.0
D

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案