题目内容
下列所给命题中,正确的有 (写出所有正确命题的序号)①任意的圆锥都存在两条母线互相垂直;
②在△ABC中,若
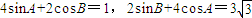 ,则∠C=30°或150°;
,则∠C=30°或150°;③关于x的二项式
 的展开式中常数项是24;
的展开式中常数项是24;④命题P:?x∈R,x2+1≥1;命题:q:?x∈R,x2-x+1≤0,则命题P∧(¬q)是真命题;
⑤已知函数
 的定义域是
的定义域是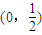 ,则实数a的取值范围是
,则实数a的取值范围是 .
.
【答案】分析:①利用特例判断正误;
②通过三角函数的平方关系式以及两角和的正弦函数,求出C的值,判断正误;
③利用二项式定理展开式,求出常数项,判断正误即可;
④通过判断命题的真假判断正误即可.
⑤通过数形结合求出a的取值范围,判断正误;
解答:解:①任意的圆锥都存在两条母线互相垂直;这是不正确的.圆锥的顶角小于90°时就没有了.
②4sinA+2cosB=1,2sinB+4cosA=3 ,∴16sin2A+4cos2B+16sinAcosB=1,①
,∴16sin2A+4cos2B+16sinAcosB=1,①
4sin2B+16cos2A+16sinBcosA=27②
①+②得16+4+16sin(A+B)=28,
∴sin(A+B)=sin(π-C)=sinC= ,所以C=30°,故②不正确;
,所以C=30°,故②不正确;
③解:二项展开式的通项为Tr+1=(-1)r24-rC4rx4-2r,令4-2r=0得r=2
所以展开式的常数项为4C42=24;正确.
④命题P:?x∈R,x2+1≥1;命题:q:?x∈R,x2-x+1≤0,则命题P∧(¬q)是真命题;正确.
⑤因为-x2+logax>0在 x∈(0, )上恒成立,即logax>x2恒成立,如图:
)上恒成立,即logax>x2恒成立,如图:
当a>1时不符合要求;
当0<a<1时,若y=logax过点( ,
, ),
),
即 =loga
=loga ,所以a=,故
,所以a=,故  ≤a<1,
≤a<1,
综上所述,a的范围为:[ ,1),所以⑤不正确.
,1),所以⑤不正确.
故答案为:③④.
点评:本题考查二项式定理,复合命题的真假,两角和与差的正弦函数的应用,考查基本知识的灵活运用,计算能力.
②通过三角函数的平方关系式以及两角和的正弦函数,求出C的值,判断正误;
③利用二项式定理展开式,求出常数项,判断正误即可;
④通过判断命题的真假判断正误即可.
⑤通过数形结合求出a的取值范围,判断正误;
解答:解:①任意的圆锥都存在两条母线互相垂直;这是不正确的.圆锥的顶角小于90°时就没有了.
②4sinA+2cosB=1,2sinB+4cosA=3
 ,∴16sin2A+4cos2B+16sinAcosB=1,①
,∴16sin2A+4cos2B+16sinAcosB=1,①4sin2B+16cos2A+16sinBcosA=27②
①+②得16+4+16sin(A+B)=28,
∴sin(A+B)=sin(π-C)=sinC=
 ,所以C=30°,故②不正确;
,所以C=30°,故②不正确;
③解:二项展开式的通项为Tr+1=(-1)r24-rC4rx4-2r,令4-2r=0得r=2
所以展开式的常数项为4C42=24;正确.
④命题P:?x∈R,x2+1≥1;命题:q:?x∈R,x2-x+1≤0,则命题P∧(¬q)是真命题;正确.
⑤因为-x2+logax>0在 x∈(0,
 )上恒成立,即logax>x2恒成立,如图:
)上恒成立,即logax>x2恒成立,如图:当a>1时不符合要求;
当0<a<1时,若y=logax过点(
 ,
, ),
),即
 =loga
=loga ,所以a=,故
,所以a=,故  ≤a<1,
≤a<1,综上所述,a的范围为:[
 ,1),所以⑤不正确.
,1),所以⑤不正确.故答案为:③④.
点评:本题考查二项式定理,复合命题的真假,两角和与差的正弦函数的应用,考查基本知识的灵活运用,计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 和
和 相交于点O,对于平面上任意一点M,若p、q分别是M到直线
相交于点O,对于平面上任意一点M,若p、q分别是M到直线
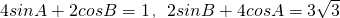 ,则∠C=30°或150°;
,则∠C=30°或150°; 的展开式中常数项是24;
的展开式中常数项是24;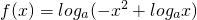 的定义域是
的定义域是 ,则实数a的取值范围是
,则实数a的取值范围是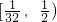 .
.