题目内容
1.已知定义在实数集R上的偶函数f(x)在区间[0,+∞)上是单调减函数.且f(2)=0.(1)求f(-2)的值;
(2)若f(1og2x)<f(2),求x的取值范围;
(3)若g(x)=$\sqrt{2}$asin(2x-$\frac{π}{3}$)+1-a,x∈[$\frac{7π}{24}$,$\frac{π}{2}$],a∈R,是否存在实数a使得f[g(x)]>0恒成立?若存在,求a的范围,若不存在说明理由.
分析 (1)利用函数奇偶性的性质即可求f(-2)的值;
(2)若f(1og2x)<f(2),结合函数奇偶性和单调性的关系将不等式进行转化即可求x的取值范围;
(3)先求出f(x)>0的解,结合三角函数的单调性进行求解即可.
解答 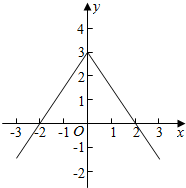 解:(1)∵函数f(x)是偶函数,
解:(1)∵函数f(x)是偶函数,
∴f(-2)=f(2)=0;
(2)若f(1og2x)<f(2),
则不等式等价为f(|1og2x|)<f(2),
∵f(x)在区间[0,+∞)上是单调减函数,
∴1og2x>2或1og2x<-2,
即x>4或0<x<$\frac{1}{4}$,
即x的取值范围是x>4或0<x<$\frac{1}{4}$;
(3)若偶函数f(x)在区间[0,+∞)上是单调减函数.且f(2)=0,
则对应的函数f(x)的图象如图:
则由f(x)>0的解为-2<x<2,
若f[g(x)]>0成立,则等价为-2<g(x)<2,
∵x∈[$\frac{7π}{24}$,$\frac{π}{2}$],
∴2x∈[$\frac{7π}{12}$,π],
2x-$\frac{π}{3}$∈[$\frac{π}{4}$,$\frac{2π}{3}$],
则sin(2x-$\frac{π}{3}$)∈[$\frac{\sqrt{2}}{2}$,1],
$\sqrt{2}$sin(2x-$\frac{π}{3}$)∈[1,$\sqrt{2}$],
①若a=0,则g(x)=1,此时满足-2<g(x)<2恒成立,
②若a>0,则g(x)∈[1,($\sqrt{2}$-1)a+1],
若-2<g(x)<2恒成立,则($\sqrt{2}$-1)a+1<2,即($\sqrt{2}$-1)a<1,得0<a<$\frac{1}{\sqrt{2}-1}$,即0<a<$\sqrt{2}$+1,
③若a<0,则g(x)∈[($\sqrt{2}$-1)a+1,1],
若-2<g(x)<2恒成立,则($\sqrt{2}$-1)a+1>-2,即($\sqrt{2}$-1)a>-3,得$-\frac{3}{\sqrt{2}-1}$<a<0,即-3($\sqrt{2}$+1)<a<0,
综上-3($\sqrt{2}$+1)<a<$\sqrt{2}$+1.
点评 本题主要考查函数奇偶性和单调性的应用,以及函数恒成立问题,根据三角函数的有界性是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
| A. | 函数不一定连续 | |
| B. | 两个端点的值不一定异号 | |
| C. | 两个端点对应的函数值的差的绝对值一定小于规定精确值 | |
| D. | 一定存在(a,b)中的一个子区间,使子区间两个端点函数值差的绝对值小于规定精确值 |
| A. | tanα | B. | tan2α | C. | $\frac{1}{3}$tan2α | D. | cotα |
 如图,已知四边形ABCD是平行四边形,O是两条对角线AC与BD的交点,设A集M={A,B,C,D,O},向量集合T={$\overrightarrow{PQ}$|P、Q∈M且P、Q不重合},求集合T中元素的个数.
如图,已知四边形ABCD是平行四边形,O是两条对角线AC与BD的交点,设A集M={A,B,C,D,O},向量集合T={$\overrightarrow{PQ}$|P、Q∈M且P、Q不重合},求集合T中元素的个数.