题目内容
如图,将边长为2,有一个锐角为60°的菱形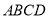 ,沿着较短的对角线
,沿着较短的对角线 对折,使得
对折,使得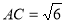 ,
,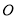 为
为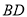 的中点.若P为AC上的点,且满足
的中点.若P为AC上的点,且满足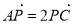 。
。

(Ⅰ)求证: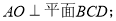
(Ⅱ)求三棱锥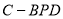 的体积;
的体积;
(Ⅰ)答案见解析;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)根据题意 和
和 是等边三角形,且
是等边三角形,且 为
为 中点,所以
中点,所以 垂直
垂直 ,再利用长度,可知
,再利用长度,可知 满足勾股定理,所以
满足勾股定理,所以 垂直
垂直 ,根据线面垂直的判定定理,结论得证;(Ⅱ)根据
,根据线面垂直的判定定理,结论得证;(Ⅱ)根据 知点为
知点为 为靠近点
为靠近点 的三等分点,所以三棱锥
的三等分点,所以三棱锥 的底面是边长为
的底面是边长为 的正三角形
的正三角形 ,高由(1)知为
,高由(1)知为 ,所以三棱锥
,所以三棱锥 的体积为
的体积为 .
.
试题解析:(Ⅰ)连接 ,由已知得
,由已知得 和
和 是等边三角形,
是等边三角形, 为
为 的中点,
的中点,
 又边长为2,
又边长为2,
由于 ,在
,在 中,
中,

 ,
,
(Ⅱ) ,
,

考点:1.线面垂直的判定定理;2.三棱锥的体积.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 B.
B.  C.
C. D.
D. 
 ,
, ,则
,则 的值为 ( )
的值为 ( ) C.7 D.
C.7 D. 
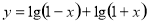 的图像关于( )
的图像关于( )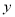 轴对称 B.
轴对称 B.  轴对称
轴对称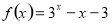 的一个零点所在的区间为( )
的一个零点所在的区间为( )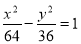 上一点,F1,F2是双曲线的两个焦点,若|PF1|=17,则|PF2|的值为________.
上一点,F1,F2是双曲线的两个焦点,若|PF1|=17,则|PF2|的值为________.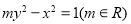 与椭圆
与椭圆 有相同的焦点,则该双曲线的渐近线方程为( )
有相同的焦点,则该双曲线的渐近线方程为( )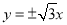 (B)
(B) (C)
(C)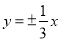 (D)
(D)