题目内容

在△ABC中，
AC
•
AB
|
AB
|
=
1
2
，
BC
•
BA
|
BA
|
=
3
2
，则AB的长为
 
．
分析：将向量
BC
用
AC
，
AB
表示，代入第二个等式，利用向量分配律展开出现第一个等式，将其值代入求出．
解答：解：∵
BC
=
AC
-
AB

∴
BC
•
BA
|
BA
|
=
(
AC
-
AB
)•
BA
|
BA
|

=
AC
•
BA
-
AB•
BA
|
BA
|
=
AC
•
BA
|
BA
|
+|
AB
|
∵
AC
•
AB
|
AB
|
=
1
2
∴
AC
•
BA
|
BA
|
= -
1
2

∵
BC
•
BA
|
BA
|
=
3
2
∴
AC
•
BA
|
BA
|
+|
AB
|=
3
2

∴AB的长为2
故答案为2
点评：本题考查平面向量基本定理：将一个向量用另一个表示；考查向量的运算律．
练习册系列答案
相关题目
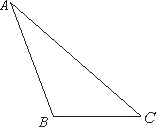精英家教网如图，在△ABC中，AC=2，BC=1，cosC=
34
．
（1）求AB的值；
（2）求sin（2A+C）的值．
在△ABC中，AC=
3
，∠A=45°，∠C=75°，则BC的长度是
 
．
精英家教网如图，在△ABC中，AC=BC，AB=2，O为AB的中点，沿OC将△AOC折起到△A′OC的位置，使得直线A′B与平面ABC成30°角．
（1）若点A′到直线BC的距离为l，求二面角A′-BC-A的大小；
（2）若∠A′CB+∠OCB=π，求BC边的长．
在△ABC中，AC=2，BC=1，sinC=
35
，则AB的长为
 
．
对于平面直角坐标系内的任意两点A（x1，y1），B（x2，y2），A（x1，y1），B（x2，y2）定义它们之间的一种“距离”：||AB||=|x2-x1|+|y2-y1|．给出下列三个命题：
①若点C在线段AB上，则||AC||+||CB||=||AB||；
②在△ABC中，||AC||+||CB||＞||AB||；
③在△ABC中，若∠A=90°，则||AB||2+||AC||2=||BC||2．
其中错误的个数为（　　）
A、0B、1C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网