Question

有一批钢管,长度都是4 000 mm,要截成500 mm和600 mm两种毛坯,且这两种毛坯数量之比按大于配套,怎样截合理?

   

Answer 1

思路分析:若设每根截500 mm的x根、600 mm的y根,

    则即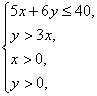

    其中x、y均为正整数,

    可行域如下图所示,

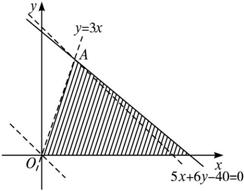
    目标函数为z=x+y,作一组平行直线x+y=t,经过可行域中的点且和原点距离最远的直线为过点A的直线.

    由得

    故A(,),

    调整为x=2,y=5,即x+y=7,经检验满足条件.

∴每根截500 mm的2根、600 mm的5根合理.

    但这是错误的.

    上述解法错误的原因是满足条件的整点不只一个,而本题只找出了满足条件的一个解.

    解:设每根截500 mm的x根、600 mm的y根,

    则且x、y∈Z.

    可行域如下图所示.

    目标函数为z=x+y,

    作一组平行直线x+y=t,

    经过可行域中的点且和原点距离最远的直线为过点B(8,0)的直线,

    这时x+y=8.

    由x、y为正整数知(8,0)并不是最优解,

    因它不在可行域内.

    因此在可行域内找整点,

    得到点(2,5),(3,4),(4,3),(5,2),(6,1)均为最优解,

    此时x+y=7.

    答:每根钢管截500 mm的2根、600 mm的5根或截500 mm的3根、600 mm的4根或截500 mm的4根、600 mm的3根或截500 mm的5根、600 mm的2根或截500 mm的6根、600 mm的1根合理.