题目内容
1.若点(16,tanθ)在函数y=log2x的图象上,则$\frac{sin2θ}{{{{cos}^2}θ}}$=( )| A. | 2 | B. | 4 | C. | 4 | D. | 8 |
分析 由已知利用对数的运算可得tanθ,再利用倍角公式及同角三角函数基本关系的运用化简即可求值.
解答 解:∵点(16,tanθ)在函数y=log2x的图象上,tanθ=${log}_{2}^{16}$,
∴解得:tanθ=4,
∴$\frac{sin2θ}{{{{cos}^2}θ}}$=$\frac{2sinθcosθ}{co{s}^{2}θ}$=2tanθ=8,
故选:D.
点评 本题主要考查了对数的运算性质,倍角公式及同角三角函数基本关系的运用,属于基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
11.如图直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB⊥AC,AA1=12,AB=3,AC=4,则球O的半径为( )
| A. | $\frac{3\sqrt{17}}{2}$ | B. | 2$\sqrt{10}$ | C. | $\frac{13}{2}$ | D. | 3$\sqrt{10}$ |
10.设函数f(x)=ex+g(x).若曲线y=g(x)在点P(0,g(0))处的切线方程是y=2x+1,则曲线y=f(x)在点Q(0,f(0))处的切线方程是( )
| A. | y=2x+1 | B. | y=2x+3 | C. | y=x+2 | D. | y=3x+2 |
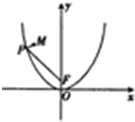 已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.
已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.