题目内容
8.在△ABC中,D是BC上一点,且B=30°,AD=5,CD=3,AC=7,求AB.分析 先在△ADC中用余弦定理求出∠ADC的余弦值,进而求出∠ADC,再根据互补求出∠ADB,然后在△ABD中用正弦定理就可求出AB的长
解答 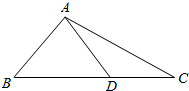 解:在△ADC中,由余弦定理得:cos∠ADC=$\frac{{3}^{2}+{5}^{2}-{7}^{2}}{2×3×5}$=-$\frac{1}{2}$
解:在△ADC中,由余弦定理得:cos∠ADC=$\frac{{3}^{2}+{5}^{2}-{7}^{2}}{2×3×5}$=-$\frac{1}{2}$
∵∠ADC∈(0,π),∴∠ADC=120°,
∴∠ADB=180°-∠ADC=60°
在△ABD中,由正弦定理得:AB=$\frac{5×\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=5$\sqrt{3}$
点评 本题考查正弦定理和余弦定理结合去解三角形,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在△ABC中,若sinA=$\frac{1}{3}$,A+B=30°,BC=4,则AB=( )
| A. | 24 | B. | 6$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 6 |
17.设函数F(x)=$\frac{f(x)}{{e}^{x}}$是定义在R上的函数,其中f(x)的导函数f′(x)满足f′(x)<f(x)对于x∈R恒成立,则( )
| A. | f(2)>e2f(0),f(2015)>e2015f(0) | B. | f(2)>e2f(0),f(2015)<e2015f(0) | ||
| C. | f(2)<e2f(0),f(2015)<e2015f(0) | D. | f(2)<e2f(0),g(2015)>e2015f(0) |