题目内容
已知圆C的圆心与椭圆| x2 |
| 25 |
| y2 |
| 24 |
分析:由椭圆的方程找出a与b的值,根据椭圆的简单性质求出c的值,得到右焦点的坐标,求此点关于y=x对称点的坐标即为圆心C的坐标;然后利用点到直线的距离公式求出圆心到已知直线的距离d,根据垂径定理及勾股定理,由弦长的一半及d的值,即可求出圆的半径r,根据圆心和半径写出圆的标准方程即可.
解答:解:由椭圆方程得到a2=25,b2=24,
根据椭圆的简单性质得:c2=a2-b2=25-24=1,解得c=1,
所以椭圆的右焦点坐标为(1,0),
又圆C的圆心与椭圆的右焦点关于直线y=x对称,
∴圆心C(0,1),
∴圆心C到直线4x-3y-2=0的距离d=
=1,又|AB|=6,
∴圆C的半径r=
=
,
则圆C的方程为:x2+(y-1)2=10.
故答案为:x2+(y-1)2=10
根据椭圆的简单性质得:c2=a2-b2=25-24=1,解得c=1,
所以椭圆的右焦点坐标为(1,0),
又圆C的圆心与椭圆的右焦点关于直线y=x对称,
∴圆心C(0,1),
∴圆心C到直线4x-3y-2=0的距离d=
| |-3-2| |
| 5 |
∴圆C的半径r=
(
|
| 10 |
则圆C的方程为:x2+(y-1)2=10.
故答案为:x2+(y-1)2=10
点评:此题考查了椭圆的简单性质,与直线y=x对称点坐标的关系,以及垂径定理及勾股定理,要求学生灵活运用点到直线的距离公式,会根据圆心和半径写出圆的标准方程.当直线与圆相交时,常常利用弦长的一半,圆的半径及弦心距构造直角三角形来解决问题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
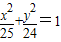 的右焦点关于直线y=x对称.直线4x-3y-2=0与圆C相交于A,B两点,且|AB|=6,则圆C的方程为 .
的右焦点关于直线y=x对称.直线4x-3y-2=0与圆C相交于A,B两点,且|AB|=6,则圆C的方程为 .