题目内容
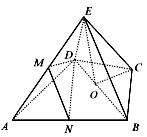
如图，几何体E-ABCD是四棱锥，△ABD为正三角形，CB=CD，EC⊥BD。
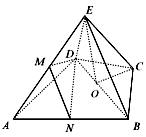
（Ⅰ）求证：BE=DE；
（Ⅱ）若∠BCD=120°，M为线段AE的中点，求证：DM∥平面BEC。
（Ⅱ）若∠BCD=120°，M为线段AE的中点，求证：DM∥平面BEC。
| 证明：（I）设BD中点为O，连接OC，OE， 则由BC=CD知，CO⊥BD， 又已知CE⊥BD，EC∩CO=C， 所以BD⊥平面OCE 所以BD⊥OE， 即OE是BD的垂直平分线， 所以BE=DE。 （II）取AB中点N，连接MN，DN， ∵M是AE的中点， ∴MN∥BE， 又MN?平面BEC，BE?平面BEC， ∴MN∥平面BEC， ∵△ABD是等边三角形， ∴∠BDN=30°， 又CB=CD，∠BCD=120°， ∴∠CBD=30°， ∴ND∥BC， 又DN?平面BEC， BC?平面BEC， ∴DN∥平面BEC， 又MN∩DN=N， 故平面DMN∥平面BEC， 又DM?平面DMN， ∴DM∥平面BEC。 |
 |
练习册系列答案
相关题目
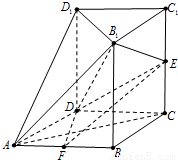
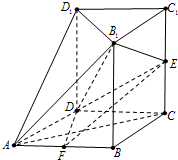（2013•青岛一模）如图，几何体ABCD-A1B1C1D1中，四边形ABCD为菱形，∠BAD=60°，AB=a，面B1C1D1∥面ABCD，BB1、CC1、DD1都垂直于面ABCD，且
（2013•青岛一模）如图，几何体ABCD-B1C1D1中，四边形ABCD为菱形，∠BAD=60°，AB=a，面B1C1D1∥面ABCD，BB1、CC1、DD1都垂直于面ABCD，且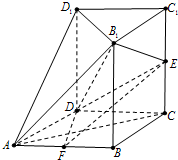
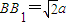，E为CC1的中点，F为AB的中点．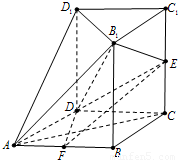
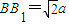，E为CC1的中点，F为AB的中点．