题目内容
【题目】
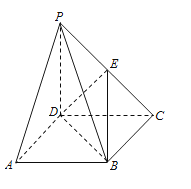
(2015·重庆)如题(20)图,三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,点D、E在线段
,点D、E在线段![]() 上,且
上,且![]() ,
,![]() 点
点![]() 在线段
在线段![]() 上,且
上,且![]()

(1)证明:![]() 平面
平面![]() .
.
(2)若四棱锥P-DFBC的体积为7,求线段BC的长。
【答案】
(1)
证明:如题(20)图。由 D E = E C , P D = P C 知, E 为等腰 △ P D C 中 D C 边的中点,故 P E ⊥ A C ,
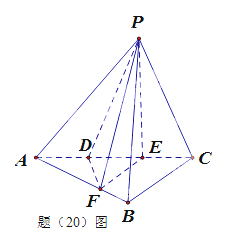
又平面![]() 平面
平面![]() ,平面
,平面![]() .
.![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,从而
,从而![]() .
.
因![]()
![]() ,故
,故![]() .
.
从而![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() ,
,![]() 都垂直,
都垂直,
所以![]() 平面
平面![]() 。
。
(2)
![]() 或
或![]() .
.
【解析】
1、证明:如题(20)图。由![]() 知,
知,![]() 为等腰
为等腰![]() 中
中![]() 边的中点,故
边的中点,故![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() .
.![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,从而
,从而![]() .
.
因![]()
![]() ,故
,故![]() .
.
从而![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() ,
,![]() 都垂直,
都垂直,
所以![]() 平面
平面![]() 。
。
2、设![]() ,则在直角
,则在直角![]() 中,
中,![]() 从而
从而![]()
由![]() ,知
,知![]() ,得
,得![]() ,故
,故![]() ,
,
即![]() 。
。
由![]() ,
,
从而四边形DFBC的面积为![]()
由小题1知,![]() 平面
平面![]() ,所以
,所以![]() 为四棱锥
为四棱锥![]() 的高。
的高。
在直角![]() 中,
中,![]() ,
,
体积![]()
故得![]() ,解得
,解得![]() 或
或![]() ,由于
,由于![]() ,可得
,可得![]() 或
或![]() 。
。
所以![]() 或
或![]() 。
。
【考点精析】解答此题的关键在于理解空间中直线与平面之间的位置关系的相关知识,掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点.

练习册系列答案
相关题目