题目内容
正△ABC边长等于
,点P在其外接圆上运动,则
?
的取值范围是( )
| 3 |
| AP |
| PB |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
分析:利用正弦定理可得△ABC的外接圆的半径R,利用外接圆的性质和数量积运算、两角和差的余弦公式、余弦函数单调性即可得出.
解答:解:如图所示.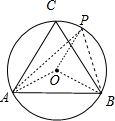
由正△ABC边长等于
,点P在其外接圆上运动.
∴∠AOB=120°,R=
=1.
∴
•
=(
-
)•(
-
)
=
•
-
2-
•
+
•
=cos∠POB-1-cos120°+cos∠AOP
=2cos∠AOBcos(∠AOP-∠POB)-
=-cos(∠AOP-∠POB)-
,
∵-1≤cos(∠AOP-∠POB)≤1,
∴
•
∈[-
,
].
故选:B.

由正△ABC边长等于
| 3 |
∴∠AOB=120°,R=
| 1 |
| 2 |
| ||
| sin60° |
∴
| AP |
| PB |
| OP |
| OA |
| OB |
| OP |
=
| OP |
| OB |
| OP |
| OA |
| OB |
| OA |
| OP |
=cos∠POB-1-cos120°+cos∠AOP
=2cos∠AOBcos(∠AOP-∠POB)-
| 1 |
| 2 |
=-cos(∠AOP-∠POB)-
| 1 |
| 2 |
∵-1≤cos(∠AOP-∠POB)≤1,
∴
| AP |
| PB |
| 3 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:本题考查了正弦定理、三角形的外接圆的性质、数量积运算、两角和差的余弦公式、余弦函数单调性等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
 如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.
如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.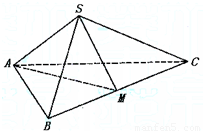 如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.
如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.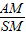 的值;
的值;