题目内容
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数 的图象.若
的图象.若 在
在 上至少含有
上至少含有 个零点,求
个零点,求 的最小值.
的最小值.
(1)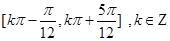 (2)
(2)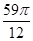
解析试题分析:
(1)要求单调区间,首先要对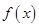 进行化简得到最间形式,依次利用正弦二倍角,降幂公式,和辅助角公式就可以得到
进行化简得到最间形式,依次利用正弦二倍角,降幂公式,和辅助角公式就可以得到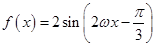 ,进而利用复合函数的单调性内外结合求得函数
,进而利用复合函数的单调性内外结合求得函数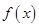 的单调区间.
的单调区间.
(2)利用“左加右减,上加下减”得到平移后的函数解析式 ,令
,令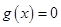 ,求出所有的零点,在根据
,求出所有的零点,在根据 上至少含有
上至少含有 个零点,得到b的取值范围,进而得到b的最小值.
个零点,得到b的取值范围,进而得到b的最小值.
试题解析:
(1)由题意得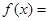
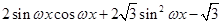
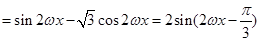 2分
2分
由周期为 ,得
,得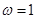 .得
.得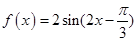 4分
4分
由正弦函数的单调增区间得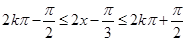 ,得
,得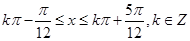
所以函数 的单调增区间是
的单调增区间是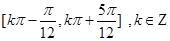 6分
6分
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移1个单位,
个单位,再向上平移1个单位,
得到 的图象,所以
的图象,所以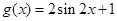 8分
8分
令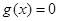 ,得:
,得: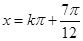 或
或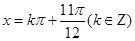 10分
10分
所以在每个周期上恰好有两个零点,若 在
在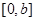 上有
上有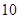 个零点,
个零点,
则 不小于第
不小于第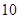 个零点的横坐标即可,即
个零点的横坐标即可,即 的最小值为
的最小值为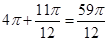 12分
12分
考点:零点 单调性 辅助角公式 正余弦倍角公式

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 .
. =-
=- ,求f(x0)的值.
,求f(x0)的值. 的图象经过点
的图象经过点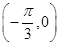 .
.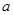 的值;
的值;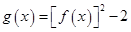 ,求函数
,求函数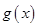 的最小正周期与单调递增区间.
的最小正周期与单调递增区间. ).
). -2f2(x)在区间
-2f2(x)在区间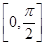 上的值域.
上的值域.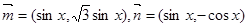 ,设函数
,设函数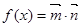 .
. 在
在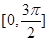 上的单调递增区间;
上的单调递增区间;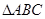 中,
中, ,
,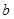 ,
,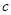 分别是角
分别是角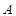 ,
,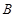 ,
,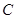 的对边,
的对边,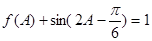 ,
,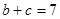 ,
,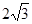 ,求边
,求边 的部分图像如图Z3-4所示,将y=f(x)的图像向右平移
的部分图像如图Z3-4所示,将y=f(x)的图像向右平移 个单位长度后得到函数y=g(x)的图像.
个单位长度后得到函数y=g(x)的图像.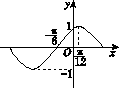
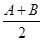 =gC+
=gC+ +1,且其外接圆半径R=2,求△ABC的面积的最大值.
+1,且其外接圆半径R=2,求△ABC的面积的最大值.
 .
. 的最小正周期和最小值;
的最小正周期和最小值;  ,
, 且
且 ,求
,求 的值.
的值.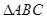 中,角
中,角 、
、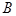 、
、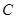 的对边分别为
的对边分别为 、
、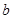 、
、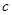 ,且
,且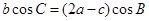 .
. 的大小;
的大小;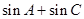 的取值范围.
的取值范围.