题目内容
如图，圆 O 的割线 PBA 过 圆心 O，弦 CD 交 PA 于点F，且△COF∽△PDF，PB ="
OA" = 2，则PF =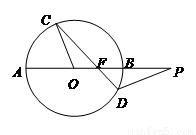 
【答案】
3
【解析】
试题分析：解：∵PB=OA=2，∴OC=OB=2，由相交弦定理得：DF?CF=AF?BF，又∵△COF∽△PDF，∴DF?CF=OF?PF，即AF?BF=OF?PF，即（4-BF）?BF=（2-BF）?（2+BF），解得BF=1，故PF=PB+BF=3，故答案为：3
考点：相交弦定理及相似三角形的性质
点评：本题考查的知识点是相交弦定理及相似三角形的性质，其中根据相交弦定理及三角形相似的性质，得到AF?BF=OF?PF，是解答本题的关键
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14、（选做题） 如图，圆 O 的割线 PBA 过圆心 O，弦 CD 交 PA 于点F，且△COF∽△PDF，PB=OA=2，则PF=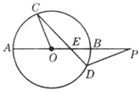
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（2011•静海县一模）如图，圆O的割线PA过圆心O交圆于另一点B，弦CD交OB于点E，且△COE∽△PDE，PB=OA=2，则PE的长等于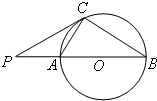
（2013•门头沟区一模）如图：圆O的割线PAB经过圆心O，C是圆上一点，PA=AC=
选做题（请考生在以下三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）