题目内容
如图,在多面体 中,四边形
中,四边形 是正方形,
是正方形, ,
, ,
, ,
,
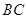 .
.

(1)求证:面 面
面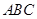 ;
;
(2)求证: 面
面 .
.
 中,四边形
中,四边形 是正方形,
是正方形, ,
, ,
, ,
,
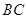 .
.
(1)求证:面
 面
面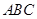 ;
;(2)求证:
 面
面 .
.(1)证明见解析;(2)见解析.
试题分析:(1)要证明面面垂直,需先证线面垂直.
利用四边形
 为正方形,证得
为正方形,证得 ,即
,即 ,
,再根据
 ,
,
 面
面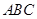
得证.
(2)注意利用“平行关系的传递性”.
通过取
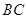 的中点
的中点 ,连结
,连结 ,
, ,
,
应用三角形中位线定理得出四边形
 为平行四边形,即
为平行四边形,即


从而得到

 面
面 ;
;类似地
 面
面 ,由面
,由面 面
面
 面
面 ,得出
,得出 面
面 .
.试题解析:证明:(1)
 四边形
四边形 为正方形,
为正方形, 
 ,
, 

 2分
2分






 4分
4分
 ,
,
 面
面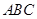
又

 面
面 ,
, 面
面 面
面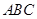 6分
6分
(2)取
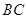 的中点
的中点 ,连结
,连结 ,
, ,
,


 ,
,
 ,
,
 四边形
四边形 为平行四边形
为平行四边形




 面
面 ,
, 面
面


 面
面 8分
8分
 ,
,
 ,
,
 四边形
四边形 为平行四边形
为平行四边形
 ,且
,且

又

 是正方形,
是正方形,
 ,且
,且


 为平行四边形,
为平行四边形,
 ,
,
 面
面 ,
, 面
面

 面
面 10分
10分
 ,
, 面
面 面
面

 面
面 ,
,
 面
面 12分
12分
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目


 .
.
 与平面
与平面 所成角的正弦值;
所成角的正弦值; 上是否存在点
上是否存在点 ?使得二面角
?使得二面角 的大小为60°,若存在,求出
的大小为60°,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. ⇒m⊥α;②
⇒m⊥α;② ⇒α⊥β;
⇒α⊥β; ⇒m∥n;④
⇒m∥n;④ ⇒m∥n
⇒m∥n


