题目内容
已知点(x,y)在圆x2+(y-1)2=1上运动.(1)求
| y-1 | x-2 |
(2)求2x+y的最大值与最小值.
分析:(1)令K=
利用斜率模型,可转化为kx-y-2k+1=0,根据圆心到直线的距离不大于半径求解.
(2)令b=2x+y利用截距模型,可转化为:2x+y-b=0,根据圆心到直线的距离不大于半径求解.
| y-1 |
| x-2 |
(2)令b=2x+y利用截距模型,可转化为:2x+y-b=0,根据圆心到直线的距离不大于半径求解.
解答:解:(1)令K=
整理得:kx-y-2k+1=0
由1≥
解得:-
≤k≤
所以
的最大值为
;最小值为-
(6分)
(2)令b=2x+y整理得2x+y-b=0
由1≥
解得:1-
≤b≤1+
所以2x+y的最大值为1+
;最小值为1-
.(12分)
| y-1 |
| x-2 |
由1≥
| |-1-2k+1| | ||
|
| ||
| 3 |
| ||
| 3 |
所以
| y-1 |
| x-2 |
| ||
| 3 |
| ||
| 3 |
(2)令b=2x+y整理得2x+y-b=0
由1≥
| |1-b| | ||
|
| 5 |
| 5 |
所以2x+y的最大值为1+
| 5 |
| 5 |
点评:本题主要考查直线与圆的位置关系其其方程的应用,是常考题型,属中档题.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 的最大值与最小值;
的最大值与最小值;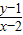 的最大值与最小值;
的最大值与最小值;