题目内容
【题目】已知直线![]() 是双曲线
是双曲线![]() 的一条渐近线,点
的一条渐近线,点![]() 在双曲线C上,设坐标原点为O.
在双曲线C上,设坐标原点为O.
(1)求双曲线C的方程;
(2)若过点![]() 的直线l与双曲线C交于R、S两点,若
的直线l与双曲线C交于R、S两点,若![]() ,求直线l的方程;
,求直线l的方程;
(3)设![]() 在双曲线上,且直线AM与y轴相交于点P,点M关于y轴对称的点为N,直线AN与y轴相交于点Q,问:在x轴上是否存在定点T,使得
在双曲线上,且直线AM与y轴相交于点P,点M关于y轴对称的点为N,直线AN与y轴相交于点Q,问:在x轴上是否存在定点T,使得![]() ?若存在,求出点T的坐标;若不存在,说明理由.
?若存在,求出点T的坐标;若不存在,说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)根据渐近线求解a,b关系,再根据双曲线上一点A求解双曲线标准方程;
(2)由![]() 知D为RS中点,利用点差法求解直线l斜率,进而求解直线方程;
知D为RS中点,利用点差法求解直线l斜率,进而求解直线方程;
(3)根据直线斜率及点斜式方程,分别列出直线AM和直线AN方程,求P,Q坐标,满足![]() ,即可求解点T坐标.
,即可求解点T坐标.
(1)由直线![]() 是双曲线渐近线,则
是双曲线渐近线,则![]() ,则双曲线方程
,则双曲线方程![]() ,
,
代入![]() ,解得
,解得![]() ,
,
故双曲线C的方程为![]()
(2)由题意,可知D为RS中点,
设RS两点坐标为![]() ,代入原式
,代入原式
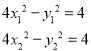 ,两式作差得
,两式作差得![]()
整理得,![]()
再由中点坐标公式![]()
解得![]()
故直线l的方程为![]()
(3)存在,
根据题意,由![]() ,则斜率
,则斜率![]() ,直线
,直线![]() ,
,
当![]() 时,
时,![]() ,即
,即![]()
同理,由![]() 则斜率
则斜率![]() ,直线
,直线![]() ,
,
当![]() 时,
时,![]() ,即
,即![]()
设:![]() ,则
,则
![]() ,
,![]() ,
,![]()
又![]() ,得到
,得到![]()
解得![]() ,又双曲线C中,
,又双曲线C中,![]() 或
或![]()
![]()
故T坐标为![]()

练习册系列答案
相关题目