题目内容
某矿山车队有4辆载重量为10 t的甲型卡车和7辆载重量为6 t的乙型卡车,有9名驾驶员.此车队每天至少要运360 t矿石至冶炼厂.已知甲型卡车每辆每天可往返6次,乙型卡车每辆每天可往返8次.甲型卡车每辆每天的成本费为252元,乙型卡车每辆每天的成本费为160元.问每天派出甲型车与乙型车各多少辆,车队所花成本费最低?
剖析:弄清题意,明确与运输成本有关的变量的各型车的辆数,找出它们的约束条件,列出目标函数,用图解法求其整数最优解.
解:设每天派出甲型车x辆、乙型车y辆,车队所花成本费为z元,那么
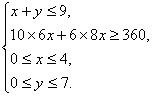
z=252x+160y,
其中x、y∈N.
作出不等式组所表示的平面区域,即可行域,如图.

作出直线l0:252x+160y=0,把直线l向右上方平移,使其经过可行域上的整点,且使在y轴上的截距最小.观察图形,可见当直线252x+160y=t经过点(2,5)时,满足上述要求.
此时,z=252x+160y取得最小值,即x=2,y=5时,zmin=252×2+160×5=1 304.
答:每天派出甲型车2辆,乙型车5辆,车队所用成本费最低.

练习册系列答案
相关题目