题目内容
已知函数 在
在 上是增函数,在
上是增函数,在 上是减函数,且
上是减函数,且 的一个根为
的一个根为
(Ⅰ)求 的值;
的值;
(Ⅱ)求证: 还有不同于
还有不同于 的实根
的实根 、
、 ,且
,且 、
、 、
、 成等差数列;
成等差数列;
(Ⅲ)若函数 的极大值小于
的极大值小于 ,求
,求 的取值范围
的取值范围
【答案】
(Ⅰ)
 是极大值点,
是极大值点, ………………2分
………………2分
(Ⅱ)令 ,得
,得 或
或
由 的单调性知
的单调性知

 是方程
是方程 的一个根,则
的一个根,则


 ………………4分
………………4分
方程 的根的判别式
的根的判别式

又 ,
,
即 不是方程
不是方程 的根
的根

 有不同于
有不同于 的根
的根 、
、 。
。

 ,
,
 、
、 、
、 成等差数列
………………8分
成等差数列
………………8分
(Ⅲ)根据函数的单调性可知 是极大值点
是极大值点

 ,于是
,于是
令
求导
 时,
时,

 在
在 上单调递减
上单调递减


即
【解析】略

练习册系列答案
相关题目
 在
在 上是增函数,
上是增函数, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 在
在 上是增函数,则
上是增函数,则 的最小值是 ( )
的最小值是 ( )
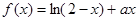 在
在 上是增函数,
上是增函数, 。当
。当 时,函数
时,函数 的最大值
的最大值 与最小值
与最小值 的差为
的差为 ,试求
,试求 的值。
的值。