题目内容
如果直线L1:y=2x+1与椭圆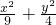 =1相交于A、B两点,直线l2与该椭圆相交于C、D两点,且ABCD是平行四边形,则l2的方程是
=1相交于A、B两点,直线l2与该椭圆相交于C、D两点,且ABCD是平行四边形,则l2的方程是
- A.y=2x
- B.y=2x-1
- C.y=2x-2
- D.y=2x+2
B
分析:由ABCD是平行四边形可知直线l1∥l2,再由l1过点(0,1),知l2过点(0,-1),由此可导出l2的方程.
解答:由题意可知,直线l1∥l2,
∴l2的斜率k=2.
∵ABCD是平行四边形,l1过点(0,1),
∴l2过点(0,-1),
∴直线l2的方程是y+1=2x,即y=2x-1.
故选B.
点评:本题考查椭圆和直线的性质,作出草图,数形结合效果好.
分析:由ABCD是平行四边形可知直线l1∥l2,再由l1过点(0,1),知l2过点(0,-1),由此可导出l2的方程.
解答:由题意可知,直线l1∥l2,
∴l2的斜率k=2.
∵ABCD是平行四边形,l1过点(0,1),
∴l2过点(0,-1),
∴直线l2的方程是y+1=2x,即y=2x-1.
故选B.
点评:本题考查椭圆和直线的性质,作出草图,数形结合效果好.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
如果直线L1:y=2x+1与椭圆
+
=1相交于A、B两点,直线l2与该椭圆相交于C、D两点,且ABCD是平行四边形,则l2的方程是( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、y=2x |
| B、y=2x-1 |
| C、y=2x-2 |
| D、y=2x+2 |


 =1相交于A、B两点,直线l2与该椭圆相交于C、D两点,且ABCD是平行四边形,则l2的方程是( )
=1相交于A、B两点,直线l2与该椭圆相交于C、D两点,且ABCD是平行四边形,则l2的方程是( )