题目内容
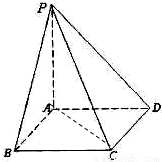
如图所示，PA⊥平面ABCD，底面ABCD为直角梯形，
，
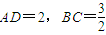，∠ADC=60°，O为四棱锥P-ABCD内一点，AO=1，若DO与平面PCD成角最小角为α，则α=（ ）
A．15°
B．30°
C．45°
D．arcsin
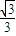
【答案】分析：根据题意，当且仅当AO⊥平面PCD时，DO与平面PCD成角最小角．利用等体积，求出AE的长，进而在△ODE中，可求DO与平面PCD成角最小角．
解答：解：根据题意，当且仅当AO⊥平面PCD时，DO与平面PCD成角最小角．
设垂足为E，连接OD，DE，则可知
∴AC⊥CD，PC⊥CD
∴
∴
∵AD=2，OA=1
∴α=15°
故选A．
点评：本题以线面垂直为载体，考查线面角，考查点面距离的求解，有一定的综合性．
解答：解：根据题意，当且仅当AO⊥平面PCD时，DO与平面PCD成角最小角．
设垂足为E，连接OD，DE，则可知
∴AC⊥CD，PC⊥CD
∴
∴
∵AD=2，OA=1
∴α=15°
故选A．
点评：本题以线面垂直为载体，考查线面角，考查点面距离的求解，有一定的综合性．
练习册系列答案
相关题目
如图所示，PA⊥平面ABCD，底面ABCD为菱形，∠ABC=60°，PA=AB=2，N为PC的中点．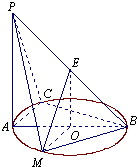
如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA=30°，PA=AB=2，，点E为线段PB的中点，点M在AB弧上，且OM∥AC．
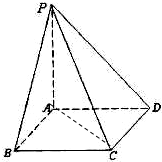如图所示，PA⊥平面ABCD，底面ABCD为直角梯形，
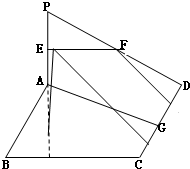如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且2PA=AD=2，E、F、G分别是线段PA、PD、CD的中点．
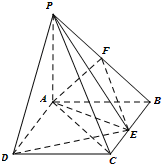如图所示，PA⊥平面ABCD，ABCD是边长为1的正方形．点F是PB的中点，点E在边BC上移动．