题目内容
记者在街上随机抽取10人,在一个月内接到的垃圾短信条数统计的茎叶图如下: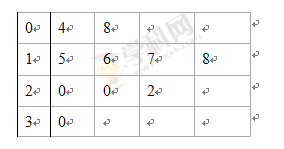
(Ⅰ)计算样本的平均数及方差;
(Ⅱ)现从10人中随机抽出2名,设选出者每月接到的垃圾短信在10条以下的人数为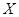 ,求随机变量
,求随机变量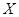 的分布列和期望.
的分布列和期望.
(Ⅰ)17, (Ⅱ)
(Ⅱ)
解析试题分析:(Ⅰ)先求平均数再求其方差。所用公式平均数 ,方差
,方差 。(Ⅱ)10人中垃圾短信在10条以下的有2人,中随机抽出2名时随机变量
。(Ⅱ)10人中垃圾短信在10条以下的有2人,中随机抽出2名时随机变量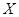 的取值为0、1、2。此概率为古典概型,基本事件总数为
的取值为0、1、2。此概率为古典概型,基本事件总数为 。随机变量
。随机变量 的基本事件数为
的基本事件数为 ,根据古典概型概率公式即可求其概率,然后可取其分布列及期望。
,根据古典概型概率公式即可求其概率,然后可取其分布列及期望。
试题解析:解:(Ⅰ)样本的平均次数为 . 3分
. 3分
样本的方差为: 
(Ⅱ)由题意,随机变量 ,
, ,
, .
. ,
, ,
,
随机变量 的分布列为
的分布列为
 . 13分
. 13分
考点:1古典概型概率,2分布列及方差。

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
为了解某市市民对政府出台楼市限购令的态度,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令的赞成人数如下表:
| 月收入 |  | [25,35) | [35,45) |  |  |  |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 8 | 5 | 2 | 1 |
(Ⅰ)根据已知条件完成下面的2×2列联表,有多大的把握认为赞不赞成楼市限购令与收入高低有关?
已知:
 ,
,当
 <2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;
<2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;当
 >2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关;
>2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关;当
 >3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关;
>3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关;当
 >6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。
>6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。| | 非高收入族 | 高收入族 | 总计 |
| 赞成 | | | |
| 不赞成 | | | |
| 总计 | | | |
 ,求n的最大值;
,求n的最大值; 、
、 、
、 的人群随机抽取
的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

 的值;
的值; 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在 的概率.
的概率.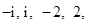 其中
其中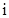 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响). 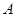 “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率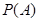 与事件
与事件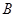 “在四次试验中,
“在四次试验中,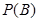 ;
;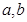 ,求随机变量
,求随机变量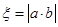 的分布列与数学期望
的分布列与数学期望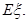
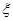 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
 分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足 的概率.
的概率.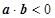 的概率.
的概率.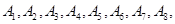 (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为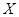 .若
.若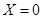 就参加学校合唱团,否则就参加学校排球队.
就参加学校合唱团,否则就参加学校排球队.