题目内容
设{an}是公比为正数的等比数列，若a3=4，a5=16，则数列{an}的前5项和为（ ）
分析：由a3=4，a5=16，可求出公比，进而得到首项，再根据前n项和公式，即可求数列的前5项和．
解答：解：由于a3=4，a5=16，则q2=
=
=4，
又由{an}是公比为正数的等比数列，则q=2．
又∵a3=4，∴a1=1，
∴数列{an}的前5项和S5=
=25-1=31．
故答案选D．
| a5 |
| a3 |
| 16 |
| 4 |
又由{an}是公比为正数的等比数列，则q=2．
又∵a3=4，∴a1=1，
∴数列{an}的前5项和S5=
| 1×(1-25) |
| 1-2 |
故答案选D．
点评：本题考查了等比数列的前n项和．要求前n项和，就要知道首项和公比．而已知条件是数列的两项，故需根据通项公式联立方程组，解出首项与公比即可．
练习册系列答案
出彩同步大试卷系列答案
相关题目
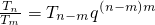（q＞0是常数）．