题目内容
12.已知函数h(x)=aex的一条切线为y=ex.(1)求a的值
(2)设x>0,求证:h(x)>1+x+$\frac{1}{2}$x2.
分析 (1)设切点,利用函数h(x)=aex的一条切线为y=ex,求a的值
(2)即证明1>(1+x+$\frac{1}{2}$x2)e-x(x>0),构造函数,即可证明.
解答 (1)解:根据题意可设切点为(x0,y0)
则$a{e}^{{x}_{0}}$=ex0,$a{e}^{{x}_{0}}$=e,
故a=1;
(2)证明:当x>0时,h(x)>1+x+$\frac{1}{2}$x2,即ex>1+x+$\frac{1}{2}$x2,
则1>(1+x+$\frac{1}{2}$x2)e-x(x>0)
令g(x)=(1+x+$\frac{1}{2}$x2)e-x,并求其最大值.
则g′(x)=(-$\frac{1}{2}$x2)e-x.
所以在x>0,g(x)恒减,所以g(x)<g(0)=1,
故h(x)>1+x+$\frac{1}{2}$x2.
点评 本题考查导数知识的运用,考查导数的几何运用,考查不等式的证明,正确转化是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7.在某校开展的“阳光体育”系列活动中,甲、乙两班之间进行了一次200米跑的团体比赛.每个班各派出5名同学比赛,讲每名同学的200米成绩记录以后(单位:秒,且已知每个成绩都是整数),总用时少的班级获胜,
成绩记录如表所示:
表格中的x∈[30,40)
(1)若x=36,从甲班的5名同学中任取3名,记这3人中用时少于乙队平均用时的人数为随机变量η,求η的分布列;
(2)若最终乙班获胜,那么当乙班同学的成绩方差最大时,x的取值是多少(直接写出结果,不用证明)?
成绩记录如表所示:
| 队员编号 | 1 | 2 | 3 | 4 | 5 |
| 甲班成绩 | 31 | 34 | 33 | 29 | 28 |
| 乙班成绩 | 27 | 31 | 30 | X | 31 |
(1)若x=36,从甲班的5名同学中任取3名,记这3人中用时少于乙队平均用时的人数为随机变量η,求η的分布列;
(2)若最终乙班获胜,那么当乙班同学的成绩方差最大时,x的取值是多少(直接写出结果,不用证明)?
4.已知全集U={0,1,2,3,4,5},集合M={0,1,3,5},则满足M∩A={0,3}的集合A可以是( )
| A. | {0,2,3} | B. | {0,3,5} | C. | {0,1,2,3} | D. | {0,2,3,5} |
1.设f(x)=|lgx|,a,b满足f(a)=f(b)=2f($\frac{a+b}{2}$)的实数,其中0<a<b,则4b-b2的取值范围是( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
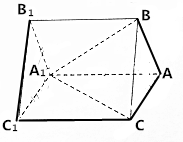 在三棱柱ABC-A1B1C1中已知AB=AC=AA1=2,∠BAA1=∠CAA1=60°,异面直线A1C1与BC成角为45°.
在三棱柱ABC-A1B1C1中已知AB=AC=AA1=2,∠BAA1=∠CAA1=60°,异面直线A1C1与BC成角为45°.