题目内容
已知与圆C:x2+y2-2x-2y+1=0相切的直线l交x轴、y轴于A、B两点,O为坐标原点,且|OA|=a,|OB|=b
(a>2,b>2).
(1)求直线l与圆C相切的条件;
(2)在(1)的条件下,求线段AB的中点轨迹方程;
(3)在(1)的条件下,求△AOB面积的最小值.
解:设直线l的方程为 ,即bx+ay-ab=0,圆C的标准方程为(x-1)2+(y-1)2=1,圆心C(1,1),半径r=1.
,即bx+ay-ab=0,圆C的标准方程为(x-1)2+(y-1)2=1,圆心C(1,1),半径r=1.
(1)直线l与圆C相切,则 ,∴(a-2)(b-2)=2(4分)
,∴(a-2)(b-2)=2(4分)
(2)设线段AB的中点M(x,y),则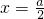 ,
, ,即a=2x,b=2y,代入(a-2)(b-2)=2,得
,即a=2x,b=2y,代入(a-2)(b-2)=2,得 (8分)
(8分)
(3) =(a-2)+(b-2)+3
=(a-2)+(b-2)+3
当且仅当 时,△AOB的面积最小,最小值为
时,△AOB的面积最小,最小值为
分析:(1)由已知中圆C:x2+y2-2x-2y+1=0,直线交x轴、y轴于A、B两点|OA|=a,|OB|=b,我们设以分别求出直线的一般方程,和圆的标准方程,然后根据直线与圆相切,圆心到直线的距离等于半径得到结论;
(2)设线段AB的中点M(x,y),代入(1)的结论,整理后,即可得到答案;
(3) ,结合(1)的结论,及均值不等式,即可得到答案.
,结合(1)的结论,及均值不等式,即可得到答案.
点评:本题考查的知识点是直线和圆的方程的应用,轨迹方程,直线与圆的位置关系,考查的解题方法为坐标法,难度中等.
 ,即bx+ay-ab=0,圆C的标准方程为(x-1)2+(y-1)2=1,圆心C(1,1),半径r=1.
,即bx+ay-ab=0,圆C的标准方程为(x-1)2+(y-1)2=1,圆心C(1,1),半径r=1.(1)直线l与圆C相切,则
 ,∴(a-2)(b-2)=2(4分)
,∴(a-2)(b-2)=2(4分)(2)设线段AB的中点M(x,y),则
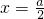 ,
, ,即a=2x,b=2y,代入(a-2)(b-2)=2,得
,即a=2x,b=2y,代入(a-2)(b-2)=2,得 (8分)
(8分)(3)
 =(a-2)+(b-2)+3
=(a-2)+(b-2)+3
当且仅当
 时,△AOB的面积最小,最小值为
时,△AOB的面积最小,最小值为
分析:(1)由已知中圆C:x2+y2-2x-2y+1=0,直线交x轴、y轴于A、B两点|OA|=a,|OB|=b,我们设以分别求出直线的一般方程,和圆的标准方程,然后根据直线与圆相切,圆心到直线的距离等于半径得到结论;
(2)设线段AB的中点M(x,y),代入(1)的结论,整理后,即可得到答案;
(3)
 ,结合(1)的结论,及均值不等式,即可得到答案.
,结合(1)的结论,及均值不等式,即可得到答案.点评:本题考查的知识点是直线和圆的方程的应用,轨迹方程,直线与圆的位置关系,考查的解题方法为坐标法,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目