题目内容
5．已知F1，F2是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右焦点，点A（1，$\frac{3}{2}$），则∠F1AF2的角平分线l所在直线的斜率为2．′．分析 推导出AF2⊥x轴，从而|AF2|=$\frac{3}{2}$，|AF1|=$\frac{5}{2}$，点F1（-1，0）关于l对称的点${{F}_{1}}^{'}$在线段AF2的延长线上，|F1′F2|=1，由此能求出∠F1AF2的角平分线l所在直线的斜率．
解答 
解：∵A（1，$\frac{3}{2}$），F1，F2是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右焦点
∴F2（1，0），
∴AF2⊥x轴，
∴|AF2|=$\frac{3}{2}$，|AF1|=$\frac{5}{2}$，
∴点F1（-1，0）关于l对称的点${{F}_{1}}^{'}$在线段AF2的延长线上，
又|AF1′|=|AF1|=$\frac{5}{2}$，∴|F1′F2|=1，
∴${{F}_{1}}^{'}$（1，-1），线段F1′F1的中点（0，-$\frac{1}{2}$），
∴k1=$\frac{\frac{3}{2}-（-\frac{1}{2}）}{1-0}$=2．
故答案为：2．
点评 本题考查∠F1AF2的角平分线l所在直线的斜率的求法，是中档题，解题时要认真审题，注意椭圆性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
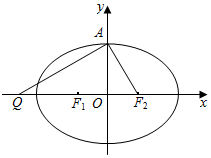设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1，F2，上顶点为A，过点A与AF2垂直的直线交x轴负半轴于点Q，且F1恰是QF2的中点．若过A、Q、F2三点的圆恰好与直线l：x-$\sqrt{3}$y-3=0相切．
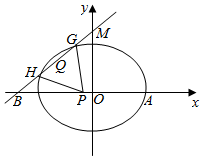已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$过点A（2，0），离心率$e=\frac{1}{2}$，斜率为k（0＜k≤1）直线l过点M（0，2），与椭圆C交于G，H两点（G在M，H之间），与x轴交于点B．
已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的右焦点到直线x-y+3$\sqrt{2}$=0的距离为5，且椭圆的一个长轴端点与一个短轴端点间的距离为$\sqrt{10}$．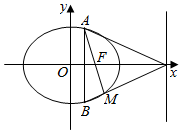
如图，已知椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，F为该椭圆的右焦点，若AB为垂直于x轴的动弦，直线l：x=4与x轴交于点N，直线AF与BN交于点M（x0，y0）．