题目内容
对于函数![]() ,若存在
,若存在![]() ∈R,使
∈R,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
如果函数![]() =
=![]() 有且仅有两个不动点0和2.
有且仅有两个不动点0和2.
(1)试求b、c满足的关系式;
(2)若c=2时,各项不为零的数列{an}满足4Sn·![]() =1,
=1,
求证: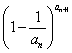 <
<![]() <
<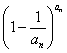 ;
;
(3)在(2)的条件下, 设bn=-![]() ,
,![]() 为数列{bn}的前n项和,
为数列{bn}的前n项和,
求证:![]() .
.
解: (1)设![]()
∴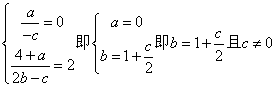
(2)∵c=2 ∴b=2 ∴![]() ,
,
由已知可得2Sn=an-an2……①,且an ≠ 1.
当n ≥ 2时,2 Sn -1=an-1-![]() ……②,
……②,
①-②得(an+an-1)( an-an-1+1)=0,
∴an=-an-1 或 an=-an-1 =-1,
当n=1时,2a1=a1-a12 ![]() a1=-1,
a1=-1,
若an=-an-1,则a2=1与an ≠ 1矛盾.∴an-an-1=-1, ∴an=-n.
∴要证不等式,只要证 ![]() ,即证
,即证 ![]() ,
,
只要证 ![]() ,即证
,即证 ![]() .
.
考虑证不等式![]() (x>0) . (**)
(x>0) . (**)
令g(x)=x-ln(1+x), h(x)=ln(x+1)-![]() (x>0) .
(x>0) .
∴![]() =
=![]() ,
, ![]() =
=![]() ,
,
∵x>0, ∴![]() >0,
>0, ![]() >0,∴g(x)、h(x)在(0, +∞)上都是增函数,
>0,∴g(x)、h(x)在(0, +∞)上都是增函数,
∴g(x)>g(0)=0, h(x)>h(0)=0,∴x>0时,![]() .
.
令![]() 则(**)式成立,∴
则(**)式成立,∴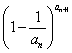 <
<![]() <
<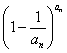 ,
,
(3)由(2)知bn=![]() ,则Tn=
,则Tn=![]() .
.
在![]() 中,令n=1,2,3,
中,令n=1,2,3,![]() ,2008,并将各式相加,
,2008,并将各式相加,
得![]() ,
,
即T2009-1<ln2009<T2008.

练习册系列答案
相关题目
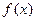 ,若存在
,若存在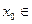 R,使
R,使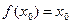 成立,则称
成立,则称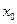 为
为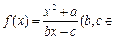 N*
N*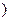 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且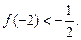
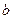 ,
,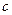 的值;
的值;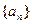
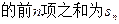 ,并且
,并且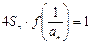 , 求数列
, 求数列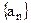 的通项公式;;
的通项公式;;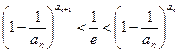 .
. ,若存在
,若存在 R,使
R,使 成立,则称
成立,则称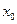 为
为 N*
N* 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且
 ,
, 的值;
的值;
 ,并且
,并且 , 求数列
, 求数列 的通项公式;;
的通项公式;;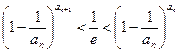 .
. ,若存在
,若存在 R,使
R,使 成立,则称
成立,则称 为
为 N*
N* 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且
 ,
, 的值;
的值;
 ,并且
,并且 , 求数列
, 求数列 的通项公式;;
的通项公式;; .
. ,若存在
,若存在 R,使
R,使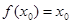 成立,则称
成立,则称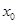 为
为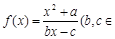 N*
N*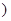 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且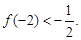
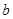 ,
,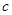 的值;
的值;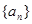
 ,并且
,并且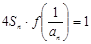 , 求数列
, 求数列 的通项公式;;
的通项公式;;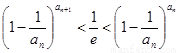 .
.